머신러닝(Machine Learning, ML)-실습

데이터 분석가:Applied Data Analytics/판다스 데이터분석

머신러닝(Machine Learning, ML)-실습

데이터분석 2025. 2. 14. 11:12

해당 실습은 정보문화사의 파이썬 머신러닝 판다스데이터분석 도서를 기반으로 정리 했습니다.

# 데이터 통계 요약정보 확인
df.describe()

# 누락 데이터 확인
df.isnull().sum() #결측치가 없다.

mpg             0
cylinders       0
displacement    0
horsepower      0
weight          0
acceleration    0
model year      0
origin          0
name            0
dtype: int64

# 중복 데이터 확인
df.duplicated().sum() #중복행이 없다

# 상관계수 분석 - 데이터프레임
corr = df.corr(numeric_only=True)
corr

# 상관계수 분석 - 히트맵
mask = np.triu(np.ones_like(corr, dtype=bool))   # 마스크 생성 (상단 트라이앵글을 숨김)

# 히트맵 그리기
plt.figure(figsize=(10, 8))
sns.heatmap(corr, mask=mask, cmap='coolwarm',
            annot=True, fmt=".2f", cbar=True, square=True)
plt.show()  #cylinders, displacement가 0.95, 0.93으로 변수의 상관계수가 높다는걸 알수 있다.

[Step 3] 데이터 전처리
'''
# horsepower 열의 고유값 확인
df['horsepower'].unique()

array(['130.0', '165.0', '150.0', '140.0', '198.0', '220.0', '215.0', '225.0', '190.0', '170.0', '160.0', '95.00', '97.00', '85.00', '88.00', '46.00', '87.00', '90.00', '113.0', '200.0', '210.0', '193.0', '?', '100.0', '105.0', '175.0', '153.0', '180.0', '110.0', '72.00', '86.00', '70.00', '76.00', '65.00', '69.00', '60.00', '80.00', '54.00', '208.0', '155.0', '112.0', '92.00', '145.0', '137.0', '158.0', '167.0', '94.00', '107.0', '230.0', '49.00', '75.00', '91.00', '122.0', '67.00', '83.00', '78.00', '52.00', '61.00', '93.00', '148.0', '129.0', '96.00', '71.00', '98.00', '115.0', '53.00', '81.00', '79.00', '120.0', '152.0', '102.0', '108.0', '68.00', '58.00', '149.0', '89.00', '63.00', '48.00', '66.00', '139.0', '103.0', '125.0', '133.0', '138.0', '135.0', '142.0', '77.00', '62.00', '132.0', '84.00', '64.00', '74.00', '116.0', '82.00'], dtype=object)

# horsepower 열의 자료형 변경 (문자열 ->숫자)
df['horsepower'] = df['horsepower'].replace('?', np.nan)      # '?'을 np.nan으로 변경
df['horsepower'] = df['horsepower'].astype('float')           # 문자열을 실수형으로 변환

df.describe()  #horsepower에만 392로 결측치가 다른컬럼에 비해 6개 존재한다.

# 결측치 제거
print(df['horsepower'].isnull().sum())
df_nan = df.dropna(subset=['horsepower'], axis=0)
print(df_nan['horsepower'].isnull().sum())

6
0

# 결측치 대체
print(df['horsepower'].isnull().sum())
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].mean())
print(df['horsepower'].isnull().sum())

6
0

# 상관계수 분석 - 데이터프레임
corr = df.corr(numeric_only=True)
corr

상관계수 분석 결과 해석

상관계수(Correlation Coefficient)는 두 변수 간의 선형 관계를 측정하는 값으로, -1에서 1 사이의 값을 가진다.

양의 상관관계(> 0): 한 변수가 증가하면 다른 변수도 증가함
음의 상관관계(< 0): 한 변수가 증가하면 다른 변수는 감소함
절댓값이 1에 가까울수록 강한 상관관계
절댓값이 0에 가까울수록 관계가 약함(거의 없음)

이제 corr 결과를 기반으로 주요 변수 간의 관계를 분석해보자.

# 분석에 활용할 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
ndf.head()

# Matplotlib으로 산점도 그리기
ndf.plot(kind='scatter', x='weight', y='mpg', c='coral', s=10, figsize=(10, 5))
plt.show()

# seaborn으로 산점도 그리기
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax1)                 # 회귀선 표시
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax2, fit_reg=False)  #회귀선 미표시
plt.show()

회귀선을 포함한 그래프(ax1)를 보면 weight가 증가할수록 mpg가 감소하는 패턴이 보일 것입니다.
이는 차량이 무거울수록 연비가 낮아지는 경향이 있다는 것을 의미합니다.
점들이 회귀선에 가깝게 분포하면 강한 선형 관계(strong correlation)를 가지며,
점들이 넓게 퍼져 있다면 약한 선형 관계(weak correlation)(무게 이외의 다른 요인에 의해 많이 영향을 받는다는 뜻)를 가집니다.
기울기가 가파르면, 무게가 연비에 강한 영향을 미친다는 뜻.
기울기가 완만하면, 영향이 약함.

# seaborn 조인트 그래프 - 산점도, 히스토그램

sns.jointplot(x='weight', y='mpg', data=ndf); # 회귀선 없음

sns.jointplot(x='weight', y='mpg', kind='reg', data=ndf); # 회귀선 표시

단순한 산점도(Scatter Plot)와 주변 분포(히스토그램)가 제공됩니다.
weight와 mpg 간의 전반적인 관계(패턴)를 확인하는 데 도움을 줍니다.
만약 데이터 점들이 뚜렷한 패턴 없이 퍼져 있다면 → 두 변수 사이에 상관관계가 약할 가능성이 높음.
반대로 데이터가 특정한 방향(예: 대각선)으로 정렬된다면 → 두 변수 간 관계가 존재할 가능성이 큼.

회귀선의 기울기를 보면, weight가 증가할 때 mpg가 감소하는지 판단할 수 있습니다.
데이터 점들이 회귀선 근처에 모여 있다면 → weight가 mpg를 설명하는 중요한 변수일 가능성이 큼.
점들이 회귀선에서 멀리 퍼져 있다면 → weight 외에도 mpg를 결정하는 다른 요인이 많을 가능성이 큼.

회귀선의 기울기
- 음의 기울기(↘️) → weight가 증가하면 mpg가 감소함 (음의 상관관계).
- 양의 기울기(↗️) → weight가 증가하면 mpg도 증가함 (양의 상관관계, 하지만 차량 연비에서는 거의 없음).
- 수평선(→) → weight와 mpg 사이에 관계가 거의 없음.
잔차(Residuals) 확인 가능
- 데이터 점들이 회귀선 주변에 밀집 → 회귀 모델이 적절함.
- 데이터 점들이 크게 퍼져 있음 → 선형 회귀보다 더 복잡한 모델이 필요할 수 있음.

연비(mpg)와 차량 무게(weight) 사이에 관계가 있는가?
- 점들이 특정한 방향(대각선)으로 정렬 → 관계 있음.
- 점들이 무작위로 퍼짐 → 관계가 약하거나 없음.
회귀선을 보고 관계의 강도를 판단할 수 있는가?
- 점들이 회귀선에 가까움 → weight가 mpg를 설명하는 중요한 변수.
- 점들이 회귀선에서 멀리 퍼짐 → mpg를 결정하는 다른 중요한 변수들이 존재함.
변수의 개별 분포를 분석할 수 있는가?
- 히스토그램을 보면 특정 구간에 데이터가 집중되어 있는지 확인 가능
- 특정 구간에 데이터가 많다면, 특정 차량 무게대에서 연비가 유사한 패턴을 가질 수 있음.

Step 4: 데이터셋 구분 - 훈련용(train data)/ 검증용(test data)
'''
# 속성(변수) 선택
X=ndf[['weight']]  #독립 변수 X
y=ndf['mpg']       #종속 변수 Y

# train data 와 test data로 구분(7:3 비율)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,               #독립 변수
                                                    y,               #종속 변수
                                                    test_size=0.3,   #검증 30%
                                                    random_state=10) #랜덤 추출 값

print('train data 개수: ', len(X_train))
print('test data 개수: ', len(X_test))

train data 개수:  278
test data 개수:  120

Step 5: 단순회귀분석 모델 - sklearn 사용
'''
# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기
from sklearn.linear_model import LinearRegression

# 단순회귀분석 모델 객체 생성
lr = LinearRegression()

# train data를 가지고 모델 학습
lr.fit(X_train, y_train)

# 학습을 마친 모델에 test data를 적용하여 결정계수(R-제곱) 계산
r_square = lr.score(X_test, y_test)
print('R^2 결정계수: ', r_square)

R^2 결정계수:  0.689363809315209

# 회귀식의 기울기
print('기울기 a: ', lr.coef_)

# 회귀식의 y절편
print('y절편 b', lr.intercept_)

기울기 a:  [-0.0076554]
y절편 b 46.60365052224634

# 모델에 test data 데이터를 입력하여 예측한 값 y_hat을 실제 값 y와 비교
y_hat = lr.predict(X_test)

# 오차 계산
test_preds = pd.DataFrame(y_test)
test_preds.columns = ['y_test']
test_preds['y_hat'] = y_hat
test_preds['squared_error'] = (test_preds['y_hat'] - test_preds['y_test'])**2
test_preds

# 평균 제곱 오차
mse = test_preds['squared_error'].mean()
print('mse: ', mse)

mse:  17.898336128759958

# 오차 분석
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.regplot(x='y_test', y='y_hat', data=test_preds, ax=axes[0]);
sns.kdeplot(x='squared_error', data=test_preds, ax=axes[1]);

첫 번째 그래프 (sns.regplot)
→ y_test(실제값)와 y_hat(예측값) 사이의 관계를 시각화 (회귀선 포함 산점도)
두 번째 그래프 (sns.kdeplot)
→ squared_error(예측 오차의 제곱)의 분포를 시각화 (밀도 함수 그래프)

(1) 첫 번째 그래프: 예측값 vs. 실제값 (sns.regplot)

x = y_test, y = y_hat → 실제값과 예측값 간의 관계를 보여줌.
회귀선(Regression Line)이 포함되어 있어, 이상적인 예측일 경우 데이터가 어떻게 분포해야 하는지 확인 가능.

(1-1) 데이터가 회귀선에 가깝게 모여 있다면?

예측값(y_hat)이 실제값(y_test)과 매우 유사함 → 모델의 성능이 좋음.
점들이 45도 기울기의 직선을 따른다면, 예측값이 거의 정확하다는 의미.

(1-2) 데이터가 회귀선에서 멀리 퍼져 있다면?

예측값과 실제값 간의 차이가 크다는 뜻 → 모델이 부정확할 가능성이 높음.
예측값이 특정 방향으로 치우쳐 있으면 편향(Bias)이 존재함을 의미함.
예를 들어, 모든 예측값이 실제값보다 작다면 모델이 체계적으로 값을 과소평가(Underestimate)하고 있음을 나타냄.

(1-3) 데이터가 랜덤하게 퍼져 있다면?

모델이 예측을 잘 못하고 있음.
예측값이 실제값과 아무런 관계 없이 분포하는 경우, 모델의 신뢰도가 낮음.

(2) 두 번째 그래프: 오차 분포 (sns.kdeplot)

x = squared_error → 예측 오차(잔차)의 제곱 값을 사용하여 모델의 예측 오차 분포를 시각화함.
밀도 그래프(KDE, Kernel Density Estimation)는 데이터의 분포 형태를 부드럽게 표현하는 그래프임.

(2-1) 분포가 좁고 0에 가까운 값에 집중되어 있다면?

대부분의 예측 오차가 작음 → 모델이 비교적 정확한 예측을 수행.
모델의 신뢰도가 높고, 과적합(Overfitting) 문제도 크지 않을 가능성이 있음.

(2-2) 분포가 넓고 오차가 큰 값까지 퍼져 있다면?

모델의 예측 오차가 크거나 일정하지 않음.
특정한 데이터 포인트에서 큰 오차를 발생시키는 경우가 많음.
모델이 일부 데이터에서 심각한 예측 오류를 내고 있을 가능성이 높음.

(2-3) 분포가 비대칭이라면?

오른쪽으로 긴 꼬리를 가진다면 (Positive Skewed)
- 일부 예측값에서 큰 오차가 발생함.
- 모델이 특정 데이터에서 예측을 크게 틀리는 경우가 많음.
좌우 대칭이면
- 모델이 특정 방향으로 편향되지 않고 있음.

모델의 예측이 실제값과 얼마나 유사한가?
- 첫 번째 그래프에서 점들이 회귀선 근처에 밀집 → 모델 성능이 좋음.
- 점들이 회귀선에서 멀리 퍼짐 → 예측이 불안정하거나 정확하지 않음.
예측 오차의 분포가 정상적인가?
- 두 번째 그래프에서 오차가 0에 가깝고 좁은 분포 → 모델이 대부분의 예측에서 정확함.
- 분포가 넓고 큰 오차가 많다면 → 모델의 예측이 불안정하거나 특정 상황에서 실패함.
예측이 체계적으로 편향되어 있는가?
- 첫 번째 그래프에서 예측값이 한쪽으로 치우쳐 있으면, 모델이 특정한 방향으로 편향(Bias)을 가지고 있음.
- 두 번째 그래프에서 오차 분포가 비대칭이면, 특정 상황에서 모델이 더 많은 오류를 내고 있을 가능성이 있음.

1. 연비(mpg)와 다른 변수 간의 관계

변수 / 상관계수(mpg) / 해석

cylinders	-0.775	실린더 개수가 많을수록 연비가 낮아짐
displacement	-0.804	배기량이 클수록 연비가 낮아짐
horsepower	-0.771	마력이 클수록 연비가 낮아짐
weight	-0.832	무거운 차일수록 연비가 낮아짐
acceleration	0.420	가속 성능이 좋을수록 연비가 높아지는 경향
model year	0.579	연식이 최신일수록 연비가 높아짐
origin	0.563	원산지(아마 일본/유럽)이 연비와 관련 있음

주요 해석

연비(mpg)는 cylinders, displacement, horsepower, weight와 강한 음의 상관관계를 가진다.
- 실린더가 많고, 배기량이 크고, 마력이 높고, 무게가 무거운 차량일수록 연비가 낮아짐.
- 즉, 고성능 차량일수록 연비가 나쁨.
연비(mpg)는 model year와 양의 상관관계를 가짐.
- 차량 연식이 최신일수록 연비가 좋아짐.
- 기술 발전과 환경 규제로 인해 연비 개선이 이루어진 것으로 보임.
연비(mpg)와 origin(원산지)도 양의 상관관계를 가짐.
- 아마도 미국(1), 유럽(2), 일본(3) 중 일본/유럽 자동차가 연비가 더 좋음.
- 미국산 자동차는 전통적으로 배기량이 크고, 일본/유럽 자동차는 연비가 좋은 경향이 있음.

2. horsepower(마력)와 다른 변수 간의 관계

변수 / 상관계수 (horsepower) / 해석

cylinders	0.839	실린더 개수가 많을수록 마력이 높음
displacement	0.894	배기량이 클수록 마력이 높음
weight	0.861	무거운 차일수록 마력이 높음
acceleration	-0.684	마력이 높을수록 가속 성능은 낮아짐
model year	-0.412	차량이 최신일수록 마력이 낮아짐
origin	-0.454	원산지(아마 일본/유럽)일수록 마력이 낮음

주요 해석

마력(horsepower)은 cylinders, displacement, weight와 강한 양의 상관관계
- 실린더 개수가 많고, 배기량이 크고, 무게가 무거운 차량일수록 마력이 높음.
- 즉, 고출력 차량일수록 크고 무거움.
마력(horsepower)과 acceleration(가속력)은 강한 음의 상관관계
- 마력이 높을수록 가속 시간이 더 오래 걸림.
- 보통 마력이 높으면 가속력이 좋을 것 같지만, 무거운 차량이 많기 때문에 전체적인 상관관계는 음수로 나타남.
마력(horsepower)은 model year와 음의 상관관계
- 최신 모델일수록 마력이 낮아지는 경향이 있음.
- 연료 효율성이 강조되면서 최신 차량은 마력이 낮아지고, 연비가 좋아지는 경향.

3. weight(차량 무게)와 다른 변수 간의 관계

변수 / 상관계수 (weight) / 해석

cylinders	0.896	실린더 개수가 많을수록 무거움
displacement	0.933	배기량이 클수록 무거움
horsepower	0.861	마력이 높을수록 무거움
acceleration	-0.417	무거운 차일수록 가속 성능이 낮음
model year	-0.307	최신 차량일수록 무게가 가벼움
origin	-0.581	원산지가 일본/유럽일수록 가벼움

주요 해석

차량 무게(weight)는 cylinders, displacement, horsepower와 매우 강한 양의 상관관계
- 실린더가 많고 배기량이 클수록 무거운 차량이 많음.
- 스포츠카, 대형 세단, SUV 등이 이런 특성을 가짐.
차량 무게(weight)는 acceleration과 음의 상관관계
- 무거운 차량일수록 가속 시간이 길어짐.
- 경차나 스포츠카는 가볍고 빠르게 가속 가능하지만, 트럭이나 대형 세단은 무겁고 가속이 느림.
차량 무게(weight)는 origin과 음의 상관관계
- 일본/유럽 차일수록 가벼운 경향.
- 미국차는 무겁고 대형차가 많은 경향이 있음.

4. 추가 분석이 필요한 부분

mpg(연비)와 horsepower(마력), weight(차량 무게)의 관계를 시각적으로 분석하면 더욱 명확한 패턴을 찾을 수 있음.
import seaborn as sns

import matplotlib.pyplot as plt

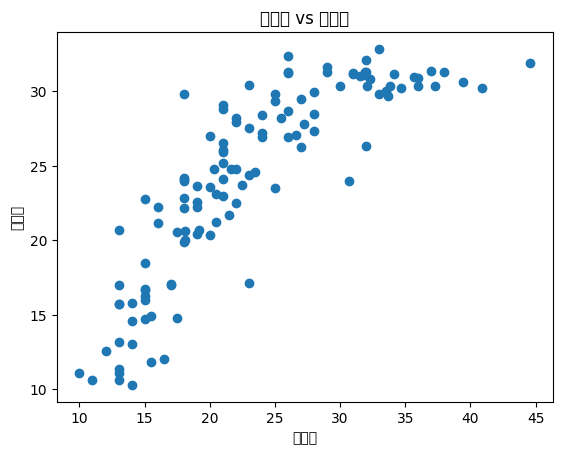
# 연비(mpg) vs 마력(horsepower) 시각화

sns.scatterplot(x=df['horsepower'], y=df['mpg'])

plt.title("마력 vs 연비")

plt.show()
→ horsepower가 증가할수록 mpg가 감소하는 경향을 확인 가능.
displacement(배기량)과 mpg(연비)의 관계도 추가 분석하면 유사한 패턴을 찾을 수 있음.
cylinders, weight, horsepower 등의 특성을 종합하여 자동차의 연비 예측 모델을 만들 수도 있음.

5. 결 론

연비(mpg)는 cylinders, displacement, horsepower, weight와 강한 음의 상관관계
- 고성능 차량일수록 연비가 나쁨
연비(mpg)는 model year와 양의 상관관계
- 최근 연식 차량일수록 연비가 좋음
마력(horsepower)과 배기량(displacement), 무게(weight)는 강한 양의 상관관계
- 출력이 높은 차량일수록 크고 무거움
일본/유럽 차량이 미국 차량보다 가볍고 연비가 좋은 경향이 있음

지금 까지는 단순회귀분석 이였으며, 이제 다항회귀분석에 대한 실습

다항 회귀 분석(Polynomial Regression)

1. 다항 회귀 분석이란?

다항 회귀 분석(Polynomial Regression)은 독립 변수(X)와 종속 변수(Y) 간의 관계가 곡선 형태인 경우 사용되는 회귀 분석 기법이다.

선형 회귀(Linear Regression)는 Y = aX + b 형태의 직선 관계를 가정하지만,
다항 회귀(Polynomial Regression)는 Y = aX² + bX + c 와 같이 곡선 관계를 가정한다.

즉, 선형 회귀가 데이터를 제대로 설명하지 못하는 경우, 다항 회귀를 적용하면 더 좋은 예측이 가능하다.

곡선 관계가 있다면 다항 회귀(Polynomial Regression)나 비선형 회귀(Nonlinear Regression) 사용

2. 다항 회귀의 핵심 개념

(1) 선형 회귀 vs. 다항 회귀

선형 회귀: 데이터를 직선(linear) 형태로 모델링
다항 회귀: 데이터를 곡선(polynomial) 형태로 모델링

(2) 다항 회귀의 수식

다항 회귀는 다항식(polynomial) 형태의 방정식을 사용한다.

Y=anXn+an−1Xn−1+...+a2X2+a1X+a0Y = a_nX^n + a_{n-1}X^{n-1} + ... + a_2X^2 + a_1X + a_0

여기서,

nn은 다항식의 차수(degree)이며, 높을수록 더 복잡한 곡선을 만들 수 있다.
a0,a1,a2,...,ana_0, a_1, a_2, ..., a_n은 회귀 계수(Weight)이다.

예를 들어,

1차 다항 회귀: Y=aX+bY = aX + b → 선형 회귀와 동일
2차 다항 회귀: Y=aX2+bX+cY = aX^2 + bX + c → 2차 함수 곡선
3차 다항 회귀: Y=aX3+bX2+cX+dY = aX^3 + bX^2 + cX + d → 더 복잡한 곡선

3. 다항 회귀 분석이 필요한 경우

(1) 선형 회귀로 데이터의 패턴을 설명할 수 없을 때

데이터가 직선이 아니라 곡선 형태로 분포할 경우 다항 회귀를 사용하면 더 적합한 모델을 만들 수 있다.

(2) 현실적인 예제

다항 회귀는 다음과 같은 데이터 패턴을 분석할 때 효과적이다.

자동차 주행 거리(X)와 연비(Y)의 관계
온도(X)와 전력 소비량(Y)의 관계
광고 비용(X)과 판매량(Y)의 관계
건물 높이(X)와 바람 속도(Y)의 관계

4. 다항 회귀 분석의 과정

(1) 데이터 준비

독립 변수(X)와 종속 변수(Y)를 준비한다.

(2) 특성 변환 (Polynomial Features)

기존의 X 데이터를 X², X³ 등 다항식 형태로 변환한다.

(3) 모델 학습

선형 회귀 모델을 사용하여 변환된 데이터를 학습한다.

(4) 모델 평가

학습된 모델이 데이터를 얼마나 잘 설명하는지 평가한다.

5. 다항 회귀 분석 구현 (Python 코드)

아래는 공부 시간(X)과 시험 점수(Y) 간의 관계를 다항 회귀로 분석하는 예제이다.

(1) 데이터 준비 및 시각화

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

from sklearn.preprocessing import PolynomialFeatures

# 데이터 생성 (공부 시간 X, 시험 점수 Y)

X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)

Y = np.array([50, 55, 65, 70, 74, 78, 80, 85, 87, 90])

# 데이터 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.title("공부 시간 vs. 시험 점수")

plt.legend()

plt.show()

(1) 변수 간의 관계 분석

점들이 대체로 우상향(↗)하는 패턴을 보이면, 공부 시간이 증가할수록 시험 점수도 증가한다는 것을 의미함.
즉, 공부 시간(X)과 시험 점수(Y) 사이에는 양의 상관관계(positive correlation)가 존재할 가능성이 높음.

(2) 관계의 강도 분석

점들이 선형 패턴(직선 형태)을 따른다면, 공부 시간이 증가할수록 일정한 비율로 점수가 상승함.
만약 점들이 완전히 직선이 아니라 곡선 형태로 분포한다면, **비선형적인 관계(예: 초반에는 점수 증가율이 낮고, 후반부에 더 가파르게 증가)**일 수도 있음.

(3) 데이터 분포 및 이상점(outliers) 확인

모든 점들이 자연스럽게 증가하는 패턴을 보이면, 정상적인 데이터라고 판단할 수 있음.
하지만 특정한 점(예: 공부 시간이 많은데 점수가 낮거나, 공부 시간이 적은데 점수가 높은 경우)이 있다면, 이는 **이상점(Outlier)**일 가능성이 있음.
이상점이 있다면 모델의 예측 성능에 영향을 미칠 수 있음.

이러한 논리적 분석을 통해, 공부 시간과 시험 점수 사이의 관계를 평가하고 적절한 모델을 선택할 수 있습니다.

1. 선형 회귀로 충분한지 확인 (산점도 분석)

해결책:

곡선 패턴이 뚜렷하면 다항 회귀를 적용
직선 패턴이라면 단순 회귀를 유지

2. 다항식 차수(degree) 설정이 적절한지 확인 (잔차 분석 & 결정계수 R² 비교)

해결책:

여러 차수 모델을 비교하여 가장 적절한 차수를 선택
과적합 방지를 위해 교차 검증(Cross Validation) 활용

3. 잔차 분석 (Residual Plot) - 등분산성(Homoscedasticity) 검토

해결책:

데이터 변환(로그 변환, Box-Cox 변환)
차수 조정(너무 높은 차수는 잔차 패턴을 왜곡할 수 있음)

4. 다항 회귀 모델이 일반화 가능성(과적합 여부) 확인

해결책:

정규화 기법 사용 (Lasso, Ridge 회귀 적용)
차수 조정 (너무 높은 차수 사용 X)

5. 다항 회귀가 필요한지 비교 (단순 회귀 vs 다항 회귀 모델 성능 비교)

해결책:

차수를 점진적으로 증가시키며 성능을 평가
필요 이상으로 높은 차수는 피하고, 적절한 차수를 선택

(2) 선형 회귀 모델 학습 (비교용)

# 선형 회귀 모델 생성 및 학습

linear_model = LinearRegression()

linear_model.fit(X, Y)

# 선형 회귀 예측

Y_pred_linear = linear_model.predict(X)

# 결과 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.plot(X, Y_pred_linear, color='red', label="Linear Regression")

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.title("선형 회귀 결과")

plt.legend()

plt.show()

(1) 데이터가 선형 관계를 가지는가?

빨간색 선(회귀선)이 데이터의 중심을 잘 통과한다면
→ 공부 시간과 시험 점수 간의 관계가 선형적(linear)일 가능성이 높음.
데이터가 직선과 크게 벗어나 있다면
→ 선형 관계가 약하거나, 비선형 관계(곡선 형태)를 가질 가능성이 있음.

(2) 모델이 데이터를 얼마나 잘 설명하는가?

점들이 빨간색 선과 가까울수록 → 모델이 데이터를 잘 설명함(예측 성능이 좋음).
점들이 선에서 멀리 떨어져 있다면 → 모델의 예측이 실제 값과 차이가 많음(예측 성능이 낮음).
잔차(Residuals):
- 잔차(실제값 - 예측값)가 작을수록 모델이 정확하게 예측하고 있음.
- 잔차가 일정한 패턴을 보이면(예: 특정 구간에서만 크거나 작다면), 모델이 특정 조건에서 부정확할 가능성이 있음.

(3) 모델이 적절한가? (비선형성 확인)

빨간색 선이 데이터의 흐름을 잘 따라가면 → 선형 회귀 모델이 적절한 선택.
빨간색 선과 점들이 많이 어긋나 있다면 →
- 데이터가 비선형적인 관계일 가능성이 높음.
- 다항 회귀(Polynomial Regression) 또는 다른 복잡한 모델이 필요할 수 있음

이러한 논리적 분석을 통해, 선형 회귀 모델의 적절성을 평가하고, 더 나은 모델을 선택할지 결정할 수 있습니다.

(3) 다항 회귀 모델 학습 및 예측

# 다항 특성 변환 (2차 다항식)

poly = PolynomialFeatures(degree=2) # 2차 다항 회귀

X_poly = poly.fit_transform(X)

# 다항 회귀 모델 생성 및 학습

poly_model = LinearRegression()

poly_model.fit(X_poly, Y)

# 다항 회귀 예측

Y_pred_poly = poly_model.predict(X_poly)

# 결과 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.plot(X, Y_pred_poly, color='green', label="Polynomial Regression (Degree=2)")

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.title("다항 회귀 결과")

plt.legend()

plt.show()

(1) 데이터가 비선형적인 패턴을 따르는가?

곡선이 데이터 패턴을 더 잘 따라가면, 다항 회귀가 선형 회귀보다 더 적절한 모델일 가능성이 높음.
만약, 데이터가 곡선 형태(즉, 일정한 증가율이 아니라 변동이 있는 패턴)를 따른다면, 다항 회귀가 선형 회귀보다 더 적절할 수 있음.

(2) 다항 회귀 모델이 데이터를 얼마나 잘 설명하는가?

곡선이 데이터에 더 가깝게 맞춰져 있다면, 모델이 데이터를 더 잘 설명하고 있는 것임.
선형 회귀보다 예측값이 실제값과 더 가까워진다면, 비선형 관계를 더 잘 포착하고 있다고 볼 수 있음.

(3) 과적합(Overfitting) 가능성

다항 회귀는 모델이 너무 복잡해지면 **데이터를 과하게 학습(Overfitting)**할 수 있음.
만약 곡선이 데이터의 작은 변화까지 과도하게 반응한다면, 학습 데이터에는 잘 맞지만 새로운 데이터에 대한 일반화 성능이 낮을 가능성이 있음.
degree=2 정도는 적절한 균형을 맞출 수 있지만, 더 높은 차수를 사용하면 과적합 가능성이 커질 수 있음.

이러한 논리적 분석을 통해, 데이터의 패턴을 파악하고, 선형 회귀와 다항 회귀 중 어떤 모델이 더 적절한지 판단할 수 있습니다

6. 다항 회귀의 장점과 단점

(1) 장점

비선형 관계를 학습할 수 있음
- 데이터가 직선이 아닌 곡선 형태일 때 선형 회귀보다 더 좋은 성능을 낼 수 있음.
간단한 데이터 변환만으로 적용 가능
- 기존 선형 회귀 모델을 확장한 방식이므로 구현이 쉬움.

(2) 단점

과적합(Overfitting) 위험
- 차수가 너무 크면(예: 5차, 6차) 데이터에 너무 민감해져 새로운 데이터에서 성능이 떨어질 수 있음.
차수 선택이 중요
- 적절한 차수를 선택하지 않으면 과적합 또는 과소적합이 발생할 수 있음.
고차원 데이터에서는 계산 비용이 증가
- 특성이 많아질수록 다항식 변환 후 데이터 차원이 커지면서 연산량이 증가.

7. 다항 회귀 분석에서 차수 선택

차수를 적절히 선택하는 것이 중요하다.

차수가 너무 낮으면(1차, 2차) → 과소적합(Underfitting) 가능성이 높음.
차수가 너무 높으면(5차, 6차 이상) → 과적합(Overfitting) 가능성이 높음.

해결 방법:

여러 차수의 모델을 만들어 성능 비교
train_test_split을 이용해 훈련 데이터와 테스트 데이터를 나누어 평가
R² Score 또는 MSE(평균 제곱 오차)를 이용해 최적의 차수 선택

8. 정리

다항 회귀 분석은 비선형적인 관계를 학습할 수 있는 회귀 분석 기법이다.
선형 회귀가 데이터를 잘 설명하지 못할 경우, 다항식 변환을 통해 곡선 형태로 모델링할 수 있다.
차수(degree)가 너무 크면 과적합이 발생할 수 있으므로 적절한 차수를 선택하는 것이 중요하다.
실제 데이터에서는 차수를 조정하면서 성능을 평가하고 최적의 모델을 선택해야 한다.

# 기본 라이브러리 불러오기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
'''
[Step 1 ~ 4] 데이터 준비
'''
# CSV 파일을 데이터프레임으로 변환
df = pd.read_csv('data/07/auto-mpg.csv', header=None)

# 열 이름 지정
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
              'acceleration','model year','origin','name']

# horsepower 열의 자료형 변경 (문자열 ->숫자)
df['horsepower'] = df['horsepower'].replace('?', np.nan)      # '?'을 np.nan으로 변경
df['horsepower'] = df['horsepower'].astype('float')           # 문자열을 실수형으로 변환

# 결측치 대체
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].mean())

# 분석에 활용할 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]

# ndf 데이터를 train data 와 test data로 구분(7:3 비율)
X=ndf[['weight']]  #독립 변수 X
y=ndf['mpg']     #종속 변수 Y

# train data 와 test data로 구분(7:3 비율)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)

print('훈련 데이터: ', X_train.shape)
print('검증 데이터: ', X_test.shape)

훈련 데이터:  (278, 1)
검증 데이터:  (120, 1)

'''
Step 5: 다항회귀분석 모형 - sklearn 사용
'''

# sklearn 라이브러리에서 필요한 모듈 가져오기
from sklearn.linear_model import LinearRegression      #선형회귀분석
from sklearn.preprocessing import PolynomialFeatures   #다항식 변환

# 다항식 변환
poly = PolynomialFeatures(degree=2)               #2차항 적용
X_train_poly=poly.fit_transform(X_train)          #X_train 데이터를 2차항으로 변형

print('원본 데이터: ', X_train.shape)
print('2차항 변환 데이터: ', X_train_poly.shape)

원본 데이터:  (278, 1)
2차항 변환 데이터:  (278, 3)

# train data를 가지고 모형 학습
pr = LinearRegression()
pr.fit(X_train_poly, y_train)

# 학습을 마친 모형에 test data를 적용하여 결정계수(R-제곱) 계산
X_test_poly = poly.fit_transform(X_test) #X_test 데이터를 2차항으로 변형
r_square = pr.score(X_test_poly,y_test)
print('R^2 결정계수: ', r_square)

R^2 결정계수:  0.72554701541758

# train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력
y_hat_test = pr.predict(X_test_poly)

fig, axes = plt.subplots(figsize=(10, 5))
axes.plot(X_train, y_train, 'o', label='Train Data') # 데이터 분포
axes.plot(X_test, y_hat_test, 'r+', label='Predicted Value') # 모형이 학습한 회귀선
axes.legend(loc='best')
plt.xlabel('weight')
plt.ylabel('mpg')
plt.show()

예측한 결과인 y_hat_test를 빨간 점(+) 으로 표시하면 회귀선이 된다.

(1) 훈련 데이터의 분포 확인

파란색 점(o)으로 표현된 훈련 데이터(X_train, y_train)를 보면,
- 데이터가 선형적으로 증가/감소하는지,
- 아니면 곡선 형태(비선형 관계)를 띄는지를 판단할 수 있음.

(2) 테스트 데이터에 대한 예측값 확인

빨간색 + 기호(r+)는 모델이 테스트 데이터(X_test)에 대해 예측한 값.
이 예측값들이 훈련 데이터의 패턴을 잘 따라가면 → 모델이 적절하게 학습되었다고 볼 수 있음.
예측값들이 훈련 데이터의 패턴과 크게 벗어나면 → 모델이 일반화 성능이 낮을 가능성이 있음.

(3) 모델의 적합성 평가

예측값(빨간색 + 기호)이 훈련 데이터 패턴과 일치하면 → 모델이 학습한 패턴이 실제 데이터와 잘 맞음.
예측값이 훈련 데이터의 패턴을 따르지 못하면 → 과소적합(Underfitting) 또는 과적합(Overfitting) 가능성 존재.

(3-1) 과소적합 (Underfitting) 가능성

예측값(빨간색 +)이 단순한 직선 형태로 나타나고, 훈련 데이터(파란색 점)의 곡선 패턴을 잘 따라가지 못하면 → 모델이 너무 단순하여 데이터 패턴을 제대로 학습하지 못한 것.
이 경우, **더 높은 차수의 다항 회귀(Polynomial Regression, degree 증가)**를 고려할 수 있음.

(3-2) 과적합 (Overfitting) 가능성

예측값(빨간색 +)이 훈련 데이터에 너무 정확히 맞춰져 있지만, 전체적인 흐름이 어색하면 → 모델이 과적합일 가능성이 있음.
이 경우, 모델의 복잡도를 줄이거나 정규화(Regularization)를 적용하는 것이 필요할 수 있음.

이러한 논리적 분석을 통해, 모델이 학습 데이터와 테스트 데이터에서 얼마나 적절한 성능을 보이는지 평가할 수 있습니다.

# 모델에 test data 데이터를 입력하여 예측한 값 y_hat_test를 실제 값 y_test와 비교
X_ploy = poly.fit_transform(X_test)

# 오차 계산
test_preds = pd.DataFrame(y_test)
test_preds.columns = ['y_test']
test_preds['y_hat'] = y_hat_test
test_preds['squared_error'] = (test_preds['y_hat'] - test_preds['y_test'])**2

# 평균 제곱 오차
mse = test_preds['squared_error'].mean()
print('mse: ', mse) #선형회귀에서는 15.814로 오차가 감소하여 결정계수가 개선된 것으로 해석 가능하다.

mse:  15.813520500520466

# 사이킷런 함수 활용 (평균 제곱 오차)
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_test, y_hat_test)
print('mse: ', mse)

mse:  15.813520500520466

# 평균 절대값 오차
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_test, y_hat_test)
print('mae: ', mae)

mae:  3.1405650734460653

# 오차 분석
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.regplot(x='y_test', y='y_hat', data=test_preds, ax=axes[0]);
sns.kdeplot(x='squared_error', data=test_preds, ax=axes[1]);

다중회귀분석 (Multiple Linear Regression)

1. 다중 회귀 분석이란?

다중 회귀 분석(Multiple Linear Regression)은 둘 이상의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 분석하는 회귀 기법이다.

단순 선형 회귀(독립 변수 1개)와 달리, 다중 회귀 분석은 여러 개의 독립 변수를 활용하여 종속 변수를 예측한다.
여러 변수들의 영향을 동시에 고려할 수 있기 때문에 보다 정교한 예측이 가능하다.

2. 다중 회귀 분석의 수식

다중 회귀는 여러 개의 독립 변수를 포함하는 선형 방정식을 기반으로 한다.

Y=a1X1+a2X2+a3X3+...+anXn+bY = a_1X_1 + a_2X_2 + a_3X_3 + ... + a_nX_n + b

YY : 종속 변수 (예측 대상)
X1,X2,X3,...,XnX_1, X_2, X_3, ..., X_n : 독립 변수 (설명 변수)
a1,a2,a3,...,ana_1, a_2, a_3, ..., a_n : 회귀 계수 (독립 변수의 영향력)
bb : 절편 (Intercept)

예를 들어, 집값 예측 모델을 만들 때

집값(Y)=a1(방개수)+a2(평수)+a3(위치)+b집값(Y) = a_1(방 개수) + a_2(평수) + a_3(위치) + b

처럼 여러 변수들을 반영할 수 있다.

3. 다중 회귀 분석이 필요한 경우

다중 회귀 분석은 하나의 변수만으로 종속 변수를 설명하기 어려울 때 사용된다.

(1) 단순 회귀로는 설명이 부족한 경우

예를 들어, 집값이 면적(㎡)만으로 결정되지 않고, 위치, 방 개수, 건축 연도 등 여러 요인이 영향을 줄 수 있음.
이러한 경우 다중 회귀 분석을 사용하여 다양한 변수의 영향을 고려하는 것이 필요하다.

(2) 현실적인 예제

집값 예측 : 면적, 방 개수, 위치 등을 이용하여 가격 예측
차량 연비 예측 : 배기량, 마력, 차량 무게 등을 이용하여 연비 예측
고객 구매 예측 : 광고 비용, 할인율, 고객 소득 수준 등을 이용하여 구매율 예측

4. 다중 회귀 분석의 과정

(1) 데이터 준비

독립 변수(X)와 종속 변수(Y)를 설정한다.

(2) 다중 회귀 모델 학습

데이터를 학습하여 회귀 계수(a1, a2, ...) 를 찾는다.

(3) 모델 평가

R² Score, MSE(평균 제곱 오차) 등을 이용하여 모델이 데이터를 얼마나 잘 설명하는지 평가한다.

(4) 변수 선택 및 최적화

독립 변수가 너무 많으면 불필요한 변수를 제거하여 모델을 단순화하는 것이 필요하다.

5. 다중 회귀 분석 구현 (Python 코드)

아래는 자동차의 배기량, 마력, 차량 무게를 이용하여 연비(MPG)를 예측하는 다중 회귀 분석 예제이다.

(1) 데이터 준비 및 전처리

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.metrics import mean_squared_error, r2_score

# 데이터 불러오기 (자동차 데이터셋 사용)

df = pd.read_csv("auto-mpg.csv")

# 독립 변수(X)와 종속 변수(Y) 설정

X = df[['displacement', 'horsepower', 'weight']] # 배기량, 마력, 차량 무게

Y = df['mpg'] # 연비 (Miles per Gallon)

# 데이터 분할 (훈련 80%, 테스트 20%)

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

(2) 다중 회귀 모델 학습

# 다중 회귀 모델 생성 및 학습

model = LinearRegression()

model.fit(X_train, Y_train)

# 예측 수행

Y_pred = model.predict(X_test)

# 회귀 계수 출력

print("회귀 계수:", model.coef_) # 독립 변수의 영향력

print("절편(Intercept):", model.intercept_) # 절편

(3) 모델 평가

# 평균 제곱 오차(MSE) 계산

mse = mean_squared_error(Y_test, Y_pred)

print(f"평균 제곱 오차(MSE): {mse:.2f}")

# 결정 계수(R² Score) 계산

r2 = r2_score(Y_test, Y_pred)

print(f"결정 계수(R² Score): {r2:.2f}")

MSE(Mean Squared Error) 값이 작을수록 모델이 정확함.
R² Score 값이 1에 가까울수록 모델이 데이터를 잘 설명함.

6. 다중 회귀 분석에서 중요한 개념

(1) 다중 공선성 (Multicollinearity) 문제

독립 변수끼리 강한 상관관계를 가지면 회귀 계수 해석이 어려워지는 문제가 발생한다.
다중 공선성이 높은 변수를 제거하는 것이 중요하다.

해결 방법:

df.corr()을 사용하여 변수 간 상관관계 확인
VIF(Variance Inflation Factor) 값을 계산하여 다중 공선성이 높은 변수를 제거
from statsmodels.stats.outliers_influence import variance_inflation_factor

# VIF 계산

vif = pd.DataFrame()

vif["Feature"] = X.columns

vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]

print(vif)
일반적으로 VIF 값이 10 이상이면 다중 공선성이 높다고 판단하여 변수를 제거하는 것이 좋다.

(2) 변수 선택 (Feature Selection)

독립 변수가 너무 많으면 모델이 복잡해지고 과적합(Overfitting) 위험이 커진다.

중요하지 않은 변수를 제거하면 모델의 성능이 향상될 수 있음.

방법:

p-value를 사용하여 통계적으로 유의미한 변수만 선택
Lasso Regression을 사용하여 중요하지 않은 변수의 계수를 자동으로 줄임

1. p-value의 개념과 사용 목적

(1) p-value란?

p-value는 귀무가설이 참이라고 가정했을 때, 현재 관찰된 데이터보다 극단적인 결과가 나타날 확률을 의미함.
즉, "이 데이터가 우연에 의해 발생할 가능성이 얼마나 되는가?"를 측정하는 지표.
p-value가 작을수록, 우연히 발생할 확률이 낮다는 의미이며, 이는 귀무가설을 기각할 근거가 더 강함을 의미함.

(2) 사용 목적

가설 검정에서 근거 기반의 결정을 내리기 위해 사용.
데이터가 단순한 우연인지, 아니면 실제로 의미 있는 차이나 관계가 있는지를 판단하는 기준.
연구 및 실험 결과를 신뢰성 있게 해석하는 데 도움을 줌.

2. p-value의 활용과 해석

(1) 가설 검정에서의 역할

통계적 가설 검정에서는 두 가지 가설이 있음:

귀무가설 (H₀): "차이가 없다" 또는 "영향이 없다"는 기본 가정.
대립가설 (H₁): "차이가 있다" 또는 "영향이 있다"는 가정.

p-value를 통해 귀무가설을 기각할지 여부를 결정함.

(2) p-value의 해석 기준

일반적으로 p-value < 0.05이면, 귀무가설을 기각하고 대립가설을 채택.
반대로 p-value ≥ 0.05이면, 귀무가설을 기각할 충분한 증거가 없다고 판단.
- 즉, 관측된 데이터가 우연에 의해 발생했을 가능성이 크므로, 유의미한 차이가 있다고 보기 어려움.

(3) 예제: 약물 실험

신약이 기존 치료제보다 효과가 있는지 실험했다고 가정.
가설 설정:
- H₀ (귀무가설): 신약과 기존 치료제의 효과 차이는 없다.
- H₁ (대립가설): 신약이 기존 치료제보다 효과가 있다.
p-value = 0.03이 나왔다면?
- 0.03 < 0.05 → 유의미한 차이가 있다고 판단
- 즉, 신약이 효과가 있다고 결론 내릴 수 있음.

3. p-value 사용 시 고려해야 할 사항

(1) p-value가 작다고 해서 무조건 인과관계가 있는 것은 아님

p-value는 통계적 연관성을 평가하는 것이지, 인과관계를 증명하는 것은 아님.
예를 들어, 아이스크림 판매량과 익사 사고 수가 높은 상관관계를 보일 수 있지만, 이것이 아이스크림이 익사의 원인이라는 의미는 아님.
즉, p-value가 낮다고 해서 무조건 "A가 B를 유발한다"는 결론을 내리면 안 됨.

(2) p-value는 샘플 크기에 영향을 받음

샘플 수가 적으면, 실제 차이가 있어도 p-value가 크게 나올 수 있음 → 차이를 감지하기 어려움.
샘플 수가 지나치게 많으면, 아주 작은 차이도 유의미하게 나올 수 있음 → 실질적으로 의미 없는 차이일 수도 있음.
따라서, 샘플 크기와 효과 크기(effect size)를 함께 고려하는 것이 중요.

(3) p-value hacking (p-hacking) 문제

연구자가 원하는 결과를 얻기 위해 여러 번 분석을 수행하고, p-value가 0.05 미만이 나올 때까지 반복적으로 실험을 조작하는 경우.
이는 통계적 유의성이 실제 의미 있는 결과를 반영하지 않을 위험을 초래.
따라서 단순히 p-value만 보고 연구 결과를 해석하면 안 되고, 연구 설계와 데이터 분석 과정도 함께 검토해야 함.

(4) p-value만으로 결정을 내리지 말 것

다른 통계 지표(R², 신뢰구간, 효과 크기 등)와 함께 해석해야 함.
예를 들어, p-value가 0.04라도 효과 크기가 매우 작다면, 실제로 유의미한 차이가 아닐 수 있음.
따라서, p-value는 결정적인 요소가 아니라 참고 지표 중 하나로 사용해야 함.

4. 최종 판단

p-value 사용의 올바른 접근법

p-value는 "귀무가설이 참일 때, 현재 데이터를 관찰할 확률"을 의미함.
일반적으로 p < 0.05면 귀무가설을 기각하지만, 무조건적인 기준이 아님.
p-value가 작아도 인과관계를 의미하지 않으며, 데이터 크기와 실질적인 의미(effect size)를 고려해야 함.
p-value만으로 결론을 내리지 말고, 신뢰구간, 효과 크기 등의 추가적인 통계적 분석과 함께 해석해야 함.

1. Lasso 회귀의 필요성

(1) 다중 공선성(Multicollinearity) 문제 해결

다중 공선성 문제란?
- 독립 변수(설명 변수)들 간에 높은 상관관계가 있으면, 모델이 불안정해지고 예측력이 저하될 수 있음.
- OLS(일반 최소제곱 회귀, Ordinary Least Squares) 모델에서는 회귀 계수(β)의 분산이 커져서 해석이 어려워지는 문제 발생.
Lasso 회귀는 불필요한 변수를 자동으로 제거하여, 다중 공선성이 심한 경우에도 안정적인 모델을 만들 수 있음.

(2) 과적합(Overfitting) 방지

일반적인 선형 회귀(OLS)는 훈련 데이터에 지나치게 적합될 위험이 있음.
특히, 독립 변수(설명 변수)의 개수가 많거나 데이터 크기가 작을 경우, 모델이 불필요한 패턴까지 학습하는 과적합(overfitting)이 발생.
Lasso는 불필요한 변수를 제거하고 중요한 변수만 남김으로써 모델을 단순화하여 과적합을 방지.

(3) 변수 선택(Feature Selection) 기능

일반적인 회귀 모델에서는 모든 변수들이 회귀 계수를 가지지만,
Lasso 회귀는 불필요한 변수의 계수를 0으로 만들어 자동으로 변수 선택(feature selection) 기능을 수행.
즉, 데이터에서 정말 중요한 변수를 찾는 데 유용.

2. Lasso 회귀의 원리

(1) L1 정규화 적용

Lasso 회귀는 L1 정규화(L1 Regularization)를 사용하여 비용 함수에 패널티(penalty) 항을 추가.
비용 함수: Loss=∑(yi−yi^)2+λ∑∣βi∣
- 첫 번째 항: 일반적인 선형 회귀의 최소제곱 오차(MSE).
- 두 번째 항: 회귀 계수(β)의 절대값 합을 최소화하는 L1 규제(L1 penalty).
- λ(람다, regularization strength): 패널티의 강도를 조절하는 하이퍼파라미터.

(2) Lasso 회귀의 특징

λ(람다) 값이 커질수록 → 모델이 더 많은 변수를 제거하여 단순한 모델이 됨.
λ(람다) 값이 작을수록 → 일반적인 선형 회귀에 가까워짐.
일부 회귀 계수(β)가 0이 됨 → 변수 선택(feature selection)이 자동으로 수행됨.

3. Lasso 회귀 사용 시 고려해야 할 사항

(1) 모든 변수의 계수가 0이 되지 않도록 λ 값을 적절히 조정해야 함

너무 큰 λ 값을 사용하면 모든 변수의 계수가 0이 되어 모델이 의미 없는 상태가 될 수 있음.
반대로, 너무 작은 λ 값을 사용하면 일반적인 선형 회귀와 동일해지며, 과적합 문제를 해결하지 못할 수 있음.

(2) 변수 선택이 필요한 경우 적합한 방법

일반적인 선형 회귀에서는 변수가 많을 경우 불필요한 변수를 제거하는 과정이 필요하지만,
Lasso 회귀는 자동으로 변수 선택을 수행하여, 유의미한 변수만 남길 수 있음.
따라서, 변수 선택(feature selection)이 필요한 경우, Lasso를 사용하면 효과적.

(3) 데이터에 따라 Lasso가 항상 최적의 방법은 아닐 수 있음

Lasso는 변수 선택 기능이 있지만, 일부 중요한 변수까지 제거할 위험이 있음.
특히, 변수 간 상관관계(Collinearity)가 높을 경우, 어떤 변수를 선택해야 할지 명확하지 않을 수 있음.
이런 경우, Ridge Regression(릿지 회귀, L2 정규화)과 비교하여 적절한 방법을 선택해야 함.

4. Lasso vs. Ridge vs. Elastic Net

Lasso는 변수를 완전히 제거할 수 있어 변수 선택에 유리하지만, 변수 간 상관관계가 높을 경우 중요한 변수를 제거할 위험이 있음.
Ridge는 모든 변수를 유지하지만 계수를 작게 조정하여 다중 공선성을 줄이는 데 효과적.
Elastic Net은 Lasso와 Ridge의 장점을 결합하여 특정 변수만 제거하면서도 안정적인 회귀 모델을 만들 수 있음.

5. 최종 판단

Lasso 회귀를 사용하는 경우

✔ 변수가 많고, 일부 불필요한 변수를 자동으로 제거하고 싶은 경우
✔ 과적합(Overfitting)을 방지하고, 중요한 변수만 남기고 싶은 경우
✔ 다중 공선성이 있는 데이터를 다룰 때 (하지만 Ridge도 함께 고려해야 함)
✔ 변수 선택(feature selection)이 필요한 경우

Lasso 회귀를 사용하지 않는 것이 좋은 경우

❌ 모든 변수가 중요하고, 변수 제거가 필요하지 않은 경우 → Ridge Regression이 더 적합
❌ 변수 간 상관관계(Collinearity)가 매우 높아 하나의 변수를 제거하면 모델이 불안정해질 경우
❌ 데이터 크기가 작고, 중요한 변수를 놓칠 위험이 있는 경우

7. 다중 회귀 분석의 장점과 단점

(1) 장점

여러 개의 변수를 고려할 수 있어 보다 정교한 예측이 가능
독립 변수와 종속 변수 간의 관계를 설명할 수 있음
해석이 용이하고, 경제·사회학 등 다양한 분야에서 활용 가능

(2) 단점

다중 공선성 문제 발생 가능
- 독립 변수끼리 상관관계가 높으면 회귀 계수 해석이 어려움.
변수가 많아지면 모델이 복잡해지고 과적합 위험 증가
선형 관계가 성립하지 않는 경우 예측 성능이 떨어질 수 있음

8. 다중 회귀 분석이 잘 맞는 경우 & 잘 안 맞는 경우

(1) 잘 맞는 경우

독립 변수와 종속 변수가 선형 관계를 가질 때
여러 요인이 종속 변수에 영향을 미치는 경우
데이터의 크기가 충분히 크고, 다중 공선성이 크지 않은 경우

(2) 잘 안 맞는 경우

독립 변수와 종속 변수 간 비선형 관계가 있는 경우
- 다항 회귀(Polynomial Regression)나 비선형 모델이 필요할 수 있음.
다중 공선성이 심한 경우
- 변수 선택이 필요함.

9. 정리

다중 회귀 분석은 두 개 이상의 독립 변수를 사용하여 종속 변수를 예측하는 회귀 기법이다.
독립 변수 간 다중 공선성을 확인하고 제거하는 것이 중요하다.
모델 평가를 위해 MSE, R² Score 등을 활용할 수 있다.
필요 없는 변수를 제거하면 모델의 성능이 향상될 수 있다.

데이터 준비

# 기본 라이브러리 불러오기

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

'''

[Step 1 ~ 3] 데이터 준비

'''

# CSV 파일을 데이터프레임으로 변환

df = pd.read_csv('data/07/auto-mpg.csv', header=None)

# 열 이름 지정

df.columns = ['mpg','cylinders','displacement','horsepower','weight',

'acceleration','model year','origin','name']

# horsepower 열의 자료형 변경 (문자열 ->숫자)

df['horsepower'] = df['horsepower'].replace('?', np.nan) # '?'을 np.nan으로 변경

df['horsepower'] = df['horsepower'].astype('float') # 문자열을 실수형으로 변환

# 결측치 대체

df['horsepower'] = df['horsepower'].fillna(df['horsepower'].mean())

# 분석에 활용할 열(속성)을 선택 (연비, 실린더, 출력, 중량)

ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]

'''

Step 4: 데이터셋 구분 - 훈련용(train data)/ 검증용(test data)

'''

# 속성(변수) 선택

X=ndf[['cylinders', 'horsepower', 'weight']] #독립 변수 X1, X2, X3

y=ndf['mpg'] #종속 변수 Y

# train data 와 test data로 구분(7:3 비율)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)

print('훈련 데이터: ', X_train.shape)

print('검증 데이터: ', X_test.shape)

훈련 데이터:  (278, 3)
검증 데이터:  (120, 3)

'''

Step 5: 다중회귀분석 모형 - sklearn 사용

'''

# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기

from sklearn.linear_model import LinearRegression

# 단순회귀분석 모형 객체 생성

lr = LinearRegression()

# train data를 가지고 모형 학습

lr.fit(X_train, y_train)

# 학습을 마친 모형에 test data를 적용하여 결정계수(R-제곱) 계산

r_square = lr.score(X_test, y_test)

print('R^2 결정계수: ', r_square)

R^2 결정계수:  0.6895968946794342

# 회귀식의 기울기

print('X 변수의 계수 a: ', lr.coef_)

# 회귀식의 y절편

print('상수항 b:', lr.intercept_)

X 변수의 계수 a:  [-0.38212538 -0.04709428 -0.00514076]
상수항 b: 46.099484743282325

# train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력

y_hat_test = lr.predict(X_test)

fig, axes = plt.subplots(1, 3, figsize=(10, 5))

for i, col in enumerate(X_test.columns):

axes[i].plot(X_train[col], y_train, 'o', label='Train Data') # 데이터 분포

axes[i].plot(X_test[col], y_hat_test, 'r+', label='Predicted Value') # 모형이 학습한 회귀선

axes[i].set_xlabel(col)

axes[i].set_ylabel(col)

axes[i].legend(loc='best')

plt.show()

(1) 변수별 관계 확인

각 그래프에서 훈련 데이터(파란색 점)와 예측값(빨간색 +)의 패턴을 비교하여,
- 해당 변수가 종속 변수(y)에 미치는 영향을 분석할 수 있음.
예를 들어, weight, horsepower, displacement 등의 독립 변수가 mpg(연비)에 어떤 영향을 주는지 개별적으로 평가 가능.

(2) 예측값이 훈련 데이터 패턴을 따르는가?

빨간색 + 기호(예측값)가 훈련 데이터 분포와 일치한다면 → 모델이 변수 간 관계를 잘 학습한 것.
빨간색 + 기호가 훈련 데이터 패턴과 다르게 분포하면 → 모델이 해당 변수의 영향을 제대로 반영하지 못할 가능성이 있음.

(3) 변수별 패턴 차이 분석

선형적인 패턴을 따르는 변수:
- X_train[col]과 y_train의 관계가 직선적인 경우 → 선형 회귀 모델이 적절할 가능성이 높음.
- 예측값(빨간색 +)이 훈련 데이터 패턴과 일치하면, 해당 변수는 선형 회귀 모델에서 중요한 설명 변수일 가능성이 있음.
비선형적인 패턴을 보이는 변수:
- X_train[col]과 y_train의 관계가 곡선 형태라면 → 단순 선형 회귀 모델로는 적절하지 않을 수 있음.
- 예측값(빨간색 +)이 데이터의 흐름을 잘 따라가지 못하면, 비선형 회귀 모델(다항 회귀, 의사결정나무 등) 또는 추가적인 변환(로그, 다항식 등)이 필요할 가능성이 있음.
예측값이 훈련 데이터 범위를 벗어나는 경우:
- 예측값이 훈련 데이터의 범위를 벗어나면, 모델이 훈련 데이터 외의 값에 대해 일반화하지 못하고 있을 가능성이 높음.
- 이는 모델이 과적합(Overfitting) 또는 과소적합(Underfitting) 상태일 가능성을 나타냄.

이러한 논리적 분석을 통해, 변수별 모델의 성능을 평가하고, 회귀 모델이 데이터를 잘 학습하고 있는지 판단할 수 있습니다.

# 사이킷런 함수 활용 (평균 제곱 오차)

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(y_test, y_hat_test)

print('mse: ', np.round(mse, 2))

# 평균 절대값 오차

from sklearn.metrics import mean_absolute_error

mae = mean_absolute_error(y_test, y_hat_test)

print('mae: ', np.round(mae, 2))

mse:  17.88
mae:  3.33

MSE (평균 제곱 오차) 공식

yiy_i : 실제값 (True Value)
y^i\hat{y}_i : 예측값 (Predicted Value)
nn : 데이터 개수
오차(예측값 - 실제값)를 제곱한 후 평균을 구하는 방식
결과값 mse:17.88
모델의 예측값과 실제값의 차이(오차)를 제곱하여 평균을 낸 값이 17.88
오차가 클수록 MSE 값이 증가 → 값이 클수록 모델의 예측이 부정확함을 의미
단위 문제: MSE는 오차를 제곱한 값이므로 실제 단위(예: 집값)가 변형됨

모델이 예측한 값과 실제 값의 평균적인 오차가 17.88² 만큼 크다는 것
오차가 클수록 MSE 값이 커지므로, 낮을수록 좋은 모델
하지만 MSE는 오차를 제곱하므로 큰 오차가 더 큰 영향을 줌
- 예를 들어, 10과 -10의 차이를 제곱하면 100이 됨
- 따라서 이상치(극단적인 오차 값)가 있을 경우 MSE가 매우 커질 가능성이 있음

MAE(평균 절대 오차) 공식

오차(예측값 - 실제값)를 절대값으로 변환 후 평균을 구하는 방식

결과값 : mae: 3.33

예측값과 실제값 간의 절대적인 평균 오차가 3.33
단위 그대로 유지됨 → 해석이 직관적

해석

모델이 예측한 값과 실제 값의 평균적인 차이가 3.33만큼 난다는 의미
MSE와 달리 제곱을 하지 않으므로 이상치에 덜 민감
낮을수록 모델이 좋은 성능을 낸다고 판단

MSE vs MAE 비교

MSE와 MAE가 모두 낮을수록 좋은 모델이지만, MSE가 MAE보다 더 큰 값으로 나왔다면, 일부 데이터에서 큰 오차가 존재할 가능성이 있음
→ 즉, 모델이 특정 데이터에서 매우 부정확한 예측을 했을 수도 있음

현재 모델 평가

MSE = 17.88 → 일부 데이터에서 큰 오차가 발생할 가능성이 있음
MAE = 3.33 → 모델이 예측한 값과 실제 값의 평균 오차가 약 3.33 단위

MSE와 MAE를 기반으로 판단할 수 있는 내용

MSE가 상대적으로 크다는 것은 일부 데이터에서 모델이 큰 오차를 보이고 있다는 뜻
- 특정 데이터 포인트에서 모델이 잘못된 예측을 하고 있을 가능성이 있음
- 이상치(Outlier) 데이터가 있는지 확인 필요
MAE가 낮으므로, 대부분의 데이터에서는 예측 성능이 괜찮음
- 대부분의 데이터에서 예측값과 실제값의 차이는 3.33 이내

추가적으로 확인해야 할 것

MSE > MAE인 경우, 이상치(Outlier)가 있는지 확인하는 것이 중요
잔차 분석 (Residual Plot)을 통해 예측값과 실제값 간의 오차 분포를 확인하면 더 명확한 해석 가능

import matplotlib.pyplot as plt

plt.scatter(y_test, y_hat_test)

plt.xlabel("실제값")

plt.ylabel("예측값")

plt.title("실제값 vs 예측값")

plt.show()

개선 방법 (MSE 줄이기)

이상치(Outlier) 처리

MSE가 크다면 이상치가 있을 가능성이 높음
이상치를 탐색 후, 제거하거나 수정 (Z-score 활용)

다양한 모델 테스트

선형 회귀 대신 Decision Tree, Random Forest 같은 다른 모델도 테스트

특성 엔지니어링 (Feature Engineering)

추가적인 변수(Feature)를 모델에 포함하면 성능이 개선될 수도 있음

정규화 / 스케일링 적용

변수 크기가 너무 차이가 난다면 StandardScaler를 적용하여 모델 성능을 향상

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

X_train_scaled = scaler.fit_transform(X_train)

X_test_scaled = scaler.transform(X_test)

MSE(평균 제곱 오차) = 17.88
- 평균적으로 예측값과 실제값 사이의 제곱 오차가 17.88
- 이상치가 존재할 가능성이 있음
- MSE는 오차를 제곱하기 때문에 큰 오차에 민감
- 값이 클수록 모델이 부정확함
MAE(평균 절대 오차) = 3.33
- 평균적으로 예측값과 실제값의 차이가 3.33
- MAE는 오차를 절대값으로 계산하므로 이상치 영향을 적게 받음
- MAE 값이 낮을수록 모델이 좋은 성능을 보임
MSE > MAE인 경우, 모델이 특정 데이터에서 큰 오차를 보일 가능성이 있음
- 잔차 분석 & 이상치 탐색 필요
- 데이터 전처리(정규화, 이상치 제거)나 모델 변경을 고려할 수 있음

MSE 값이 작으면?
- 모델이 정확한 예측을 수행하고 있음.
- 예측 오차가 작아 신뢰할 만한 모델일 가능성이 높음.
MSE 값이 크면?
- 모델의 예측이 부정확할 가능성이 높음.
- 모델을 개선하거나 다른 알고리즘을 고려할 필요가 있음.
MSE 값만으로 절대적인 판단을 할 수 있는가?
- 데이터의 크기와 단위에 따라 다를 수 있으므로 다른 모델과 비교하는 것이 중요함.
- MAE(Mean Absolute Error), RMSE(Root Mean Squared Error) 등 다른 성능 지표와 함께 고려하는 것이 좋음.

잔차 분석(Residual Plot)은 예측값과 실제값 간의 오차(잔차, Residuals)의 분포를 시각화하는 방법이다.
잔차 분석을 통해 모델이 데이터를 잘 학습했는지, 특정 패턴이 있는지, 오차가 일정하게 분포하는지 확인할 수 있다.

이러한 논리적 분석을 통해, MSE 값이 모델의 성능을 어떻게 반영하는지 판단할 수 있습니다.

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.metrics import mean_squared_error

# 예제 데이터 (실제값과 예측값)

y_test = np.array([10, 20, 30, 40, 50, 60, 70, 80, 90, 100]) # 실제값

y_hat_test = np.array([12, 18, 29, 42, 48, 58, 75, 78, 95, 98]) # 예측값

# 잔차 계산 (Residuals = 실제값 - 예측값)

residuals = y_test - y_hat_test

# MSE 계산 및 출력

mse = mean_squared_error(y_test, y_hat_test)

print(f"평균 제곱 오차(MSE): {mse:.2f}")

# 잔차 플롯 (Residual Plot)

plt.figure(figsize=(8, 5))

sns.residplot(x=y_hat_test, y=residuals, lowess=True, scatter_kws={"alpha": 0.7}, line_kws={"color": "red"})

plt.axhline(y=0, color='black', linestyle='--', linewidth=1) # y=0 기준선 추가

plt.xlabel("예측값 (Predicted Values)")

plt.ylabel("잔차 (Residuals)")

plt.title("Residual Plot (잔차 분석 그래프)")

plt.show()

※ 참고로 위 코드에서 sns.residplot() 함수에서 lowess=True 옵션을 사용하려면 statsmodels 라이브러리가 필요하다는 의미이므로 statsmodels 설치해야 됩니다.

터미널 또는 Anaconda Prompt에서 pip install statsmodels

or (Anaconda 환경이라면) conda install -c conda-forge statsmodels

결과값

Residual Plot을 통해 알 수 있는 내용
1. 잔차란?
잔차(Residuals)는 실제값과 예측값의 차이입니다. 즉, 모델이 얼마나 정확하게 예측했는지를 보여줍니다
잔차가 0에 가까울수록 모델이 실제값을 잘 예측한 것입니다.
2. MSE(Mean Squared Error) 값
코드에서 mean_squared_error()로 계산된 MSE 값을 출력합니다.
- MSE는 오차(잔차)의 제곱 평균으로, 값이 작을수록 모델이 더 정확한 예측을 했다는 의미입니다.
- mse = 16.40 (예시)라면, 평균적으로 모델의 예측이 실제값에서 약 16.4만큼 차이가 있다는 뜻입니다.
3. Residual Plot(잔차 플롯)에서 확인할 수 있는 것
잔차 플롯의 핵심은 "잔차가 특정한 패턴 없이 고르게 분포하는가?" 입니다.

(1) 잔차가 0을 중심으로 랜덤하게 분포하는가?

- 잔차가 0을 중심으로 무작위로 분포한다면, 모델이 비교적 잘 작동하고 있는 것.
- 특정한 패턴 없이 위아래로 균등하게 퍼져 있다면, 모델이 편향(Bias) 없이 데이터를 적절히 예측하고 있다는 의미.

(2) 잔차가 특정한 패턴을 보이는가?

- 잔차가 일정한 방향으로 증가하거나 감소하는 패턴을 보이면 → 모델이 체계적으로 오차를 발생시키고 있다는 뜻.
- 예를 들어, 예측값이 커질수록 잔차가 증가한다면, 모델이 큰 값을 과소평가(Underestimation)하는 경향이 있을 수 있음.
- 반대로, 예측값이 작을수록 잔차가 커진다면, 작은 값을 과대평가(Overestimation)하고 있을 가능성이 있음.

(3) 잔차의 크기가 일정한가? (등분산성, Homoscedasticity)

- 잔차의 분포가 일정하면 → 모델의 예측이 일관되며, 모든 값에 대해 비슷한 수준의 오차를 가짐.
- 만약, 예측값이 커질수록 잔차의 범위가 넓어진다면(부채꼴 형태) → 모델이 큰 값에서 더 큰 예측 오차를 보이는 것.
- 이런 경우, 데이터의 분산이 일정하지 않으므로, 모델이 특정 범위에서만 잘 작동하는 문제(Heteroscedasticity)가 발생할 수 있음.
결론
- 잔차 분석을 통해 선형 회귀 모델이 적절한지 확인하고, 필요하면 모델을 개선해야함.
- 잔차 플롯이 0을 중심으로 무작위 분포 → 모델이 적절히 예측하고 있음
- 잔차가 특정한 패턴을 보이면 → 모델의 문제점을 개선할 필요 있음
- MSE 값이 낮을수록 → 모델의 예측 정확도가 높음

이러한 분석을 통해, 모델이 예측한 값이 실제 데이터와 얼마나 잘 맞는지, 추가적인 개선이 필요한지 판단할 수 있습니다.

'데이터 분석가:Applied Data Analytics > 판다스 데이터분석' 카테고리의 다른 글

데이터분석머신러닝-실습(k-Means, DBSCAN) (0)	2025.02.17
데이터분석머신러닝-실습(KNN, SVM) (0)	2025.02.17
머신러닝(Machine Learning, ML)-용어편 (0)	2025.02.14
4. Data transformation - 영국시장의 중고 자동차 가격 데이터 다루기[프로젝트] (0)	2025.02.13
3. Data transformation (0)	2025.02.12

현재글머신러닝(Machine Learning, ML)-실습

데이터분석가 기술블로그

일정분석 전문가의 데이터분석가 기술블로그입니다.

시각화, mainquest06, mainquest, 데이터분석가, 태블로, 빅분기, 머신러닝, 건강, 데이터 시각화, SQL, 데이터시각화, 공정관리, 데이터분석, ADsP, 베트남, 파이썬, 운동, 일정관리, mq06, Tableau,

Today :
Yesterday :

« 2025/04 »
일	월	화	수	목	금	토
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30