320x100
728x90
학습목표
- 연속형 확률과 이산형 확률에 대해 이해합니다.
- 다양한 확률의 분포를 알아봅니다.
- 실습 Python 활용 다양한 분포 익히기
제이슨을 회사에서 많이 다룬다 SQL이나 파이썬에서 파씽 할 줄 알아야된다.
제이슨을 많이 다뤄보면 좋다.
JSON (JavaScript Object Notation) 이란?
1. JSON의 특징
1) 경량 데이터 포맷
- XML과 비교하여 데이터 표현이 간결하며, 파일 크기가 작음.
- 텍스트 기반이므로 사람이 읽고 이해하기 쉬움.
2) 키-값 (Key-Value) 형식
- Python의 딕셔너리(Dictionary)와 유사한 구조.
- 데이터는 "키(Key)" 와 "값(Value)" 형태로 저장됨.
3) 다양한 프로그래밍 언어에서 지원
- JSON은 Python, JavaScript, Java, C++, PHP, Go 등 대부분의 언어에서 사용 가능.
4) API와 데이터 교환에 사용
- RESTful API, 웹 애플리케이션, 데이터베이스, 설정 파일 등에서 데이터를 주고받을 때 JSON을 사용함.
2. JSON 문법 (Syntax)
JSON 데이터는 다음과 같은 형태를 가집니다.
기본 구조 (Key-Value)
json
복사편집
{
"name": "John",
"age": 25,
"city": "New York"
}
- 문자열(String)은 반드시 큰따옴표("")로 감싸야 함
- 숫자, 배열, 객체, 불리언 값도 지원함
JSON 배열 (Array)
json
복사편집
{
"employees": [
{"name": "Alice", "age": 30},
{"name": "Bob", "age": 28},
{"name": "Charlie", "age": 35}
]
}
- 배열(Array)은 리스트 형태로 여러 개의 JSON 객체를 포함 가능
3. JSON과 Python 데이터 변환
1) JSON → Python 변환 (Parsing)
Python에서 JSON 데이터를 딕셔너리(Dictionary)로 변환할 수 있음.
python
복사편집
import json
# JSON 문자열
json_data = '{"name": "John", "age": 25, "city": "New York"}'
# JSON → Python 변환
python_dict = json.loads(json_data)
print(python_dict["name"]) # 출력: John
2) Python → JSON 변환 (Encoding)
Python의 딕셔너리를 JSON 형식으로 변환 가능.
python
복사편집
import json
# Python 딕셔너리
python_dict = {"name": "John", "age": 25, "city": "New York"}
# Python → JSON 변환
json_data = json.dumps(python_dict, indent=4) # 보기 좋게 출력 (들여쓰기)
print(json_data)
4. JSON의 장점과 단점
JSON의 장점
- 경량 데이터 포맷 → XML보다 간결하고 파일 크기가 작음.
- 가독성이 높음 → 사람이 직접 읽고 수정하기 쉬움.
- 호환성이 뛰어남 → 거의 모든 프로그래밍 언어에서 사용 가능.
- 네트워크에서 빠르게 전송 가능 → API, 데이터 교환에 최적화됨.
JSON의 단점
- 데이터 타입 제한 → JSON은 숫자, 문자열, 배열, 객체, 불리언, null만 지원 (날짜 타입 없음).
- 주석 지원 X → JSON 파일 내에서 주석을 사용할 수 없음.
- 이진 데이터 저장 어려움 → 바이너리 데이터를 직접 저장하기 어려움 (Base64 인코딩 필요).
5. JSON 활용 사례
- 웹 개발 & REST API → 클라이언트-서버 간 데이터 교환 (예: 프론트엔드 ↔ 백엔드)
- 데이터베이스 (MongoDB, Firebase) → JSON 형식으로 데이터 저장
- 설정 파일 (Configuration Files) → .json 형식으로 앱 설정 저장
- 머신러닝 & 데이터 분석 → JSON 파일로 데이터 저장 후 분석
결론
- JSON은 데이터를 저장하고 교환하는 가장 인기 있는 포맷 중 하나
- 가볍고, 가독성이 좋으며, 거의 모든 프로그래밍 언어에서 지원
- 웹 개발, API, 데이터베이스, 머신러닝 등 다양한 분야에서 활용 가능
척도 :
척도(Scale)는 데이터를 측정하고 분류하는 기준을 의미합니다.
데이터를 수량화하거나 비교할 때 일정한 기준을 설정하여 측정하는 방법을 척도라고 합니다.
척도는 데이터의 특성에 따라 4가지 유형으로 나뉩니다.
1. 척도의 4가지 유형 (스티븐스의 척도)
1) 명목 척도 (Nominal Scale)
- 범주형 데이터(이름, 분류)
- 숫자가 의미가 없고, 단순히 구분하기 위한 척도
- 비교 불가능, 크기 개념 없음
✔ 예시
- 성별: 남(1), 여(2)
- 혈액형: A형, B형, O형, AB형
- 축구팀: 맨유, 리버풀, 레알 마드리드
✔ 수학적 연산 가능 여부
- 연산 불가능 (단순 분류만 가능)
- 평균, 차이 계산 불가능
- 빈도수(Count)만 분석 가능
2) 서열 척도 (Ordinal Scale)
- 순서(순위)가 있는 데이터
- 값의 크고 작음은 비교할 수 있지만, 차이의 크기는 의미 없음
- 순위는 있지만, 간격이 일정하지 않음
✔ 예시
- 만족도 조사: 매우 만족(5), 만족(4), 보통(3), 불만족(2), 매우 불만족(1)
- 성적 등급: A, B, C, D, F
- 대회 순위: 1등, 2등, 3등
✔ 수학적 연산 가능 여부
- 순위 비교 가능 (대소 비교 가능)
- 평균, 차이 계산 불가능
- 중앙값(Median) 계산 가능
3) 등간 척도 (Interval Scale)
- 순위 + 측정값 사이의 간격(차이)이 일정함
- 하지만, 절대적인 "0"의 개념이 없음
- 비율 계산 불가능 (예: 20°C는 10°C의 2배라고 할 수 없음)
✔ 예시
- 온도(°C, °F): 20°C - 10°C = 10°C (차이는 의미 있음, 하지만 0°C가 절대적 0이 아님)
- IQ 점수: 140 - 120 = 20 (차이는 일정하지만, 0 IQ가 절대적인 기준이 아님)
- 연도(Year): 2020년, 2023년 (연도 간 차이는 의미 있지만, 0년이 절대적 기준이 아님)
✔ 수학적 연산 가능 여부
- 차이 계산 가능 (덧셈, 뺄셈 가능)
- 비율 계산 불가능
- 평균, 표준편차 계산 가능
4) 비율 척도 (Ratio Scale)
- 순위 + 간격 일정 + 절대적 "0"의 기준 존재
- 비율 계산 가능 (예: 20kg는 10kg의 2배)
- 물리적 단위(길이, 무게, 속도 등)에 많이 사용됨
✔ 예시
- 키(cm), 몸무게(kg), 나이(년), 수입(원), 거리(km), 속도(m/s)
- 0kg은 진짜 무게가 없는 상태이므로, 절대적 0이 존재
- 100m 달리기 기록: 10초, 20초 → 20초는 10초의 2배
✔ 수학적 연산 가능 여부
- 덧셈, 뺄셈, 곱셈, 나눗셈 모두 가능
- 평균, 표준편차, 비율 계산 가능
2. 척도별 비교 정리
척도 유형 의미 비교 가능 여부 연산 가능 여부 예시
| 명목 척도 | 단순 분류 | ❌ 불가능 | ❌ 불가능 | 성별, 혈액형, 지역명 |
| 서열 척도 | 순위만 비교 가능 | ✅ 가능 (순위 비교) | ❌ 불가능 (차이 비교 X) | 만족도 조사, 학년, 성적 등급 |
| 등간 척도 | 크기 비교 가능, 간격 일정 | ✅ 가능 (차이 계산 가능) | ✅ 덧셈, 뺄셈 가능 (비율 계산 불가능) | 온도(°C, °F), IQ 점수, 연도 |
| 비율 척도 | 절대적 0 존재, 비율 계산 가능 | ✅ 가능 | ✅ 사칙연산 가능 | 키, 몸무게, 나이, 수입 |
3. 결론
- 명목 척도 → 단순 분류 (비교 불가능, 연산 불가능)
- 서열 척도 → 순서 있음 (순위 비교 가능, 연산 불가능)
- 등간 척도 → 차이 계산 가능 (덧셈, 뺄셈 가능, 비율 계산 불가능)
- 비율 척도 → 모든 연산 가능 (절대적 0 기준 존재)
각 척도는 데이터 분석에서 매우 중요한 개념이므로, 분석 목적에 따라 적절한 척도를 선택해야 합니다.
분포 :
분포(Distribution)란 데이터가 특정 값들을 중심으로 어떻게 퍼져 있는지를 나타내는 개념입니다.
즉, 변수가 가질 수 있는 값과 그 값이 발생할 확률 또는 빈도를 설명하는 수학적 모델입니다.
1. 분포의 기본 개념
- 데이터가 중심을 기준으로 어떻게 퍼져 있는지 시각화할 수 있음
- 평균(Mean), 중앙값(Median), 표준편차(σ) 등의 지표를 이용해 분석 가능
- 확률분포(Probability Distribution)는 특정 확률로 값이 발생하는 패턴을 설명하는 모델
2. 분포의 주요 종류
분포는 크게 **이산형 분포(Discrete Distribution)**와 **연속형 분포(Continuous Distribution)**로 나뉩니다.
1) 이산형 확률 분포 (Discrete Probability Distribution)
- 특정한 값(정수)을 가질 수 있는 확률 분포
- 예) 주사위를 던졌을 때 나올 수 있는 값 {1, 2, 3, 4, 5, 6}
✔ 대표적인 이산형 분포
분포명 특징 예시
| 베르누이 분포 | 한 번의 시행에서 성공(1) 또는 실패(0)만 존재 | 동전 던지기 |
| 이항 분포 | n번 시행에서 성공 횟수를 나타냄 | 10번 던진 동전이 앞면이 나올 횟수 |
| 포아송 분포 | 일정한 시간 동안 발생하는 사건의 개수를 나타냄 | 시간당 고객 방문 수 |
2) 연속형 확률 분포 (Continuous Probability Distribution)
- 특정 구간 내에서 모든 값(실수)을 가질 수 있는 확률 분포
- 예) 사람의 키(170.5cm 가능), 온도(36.6°C 가능)
✔ 대표적인 연속형 분포
분포명 특징 예시
| 정규 분포 | 평균을 중심으로 대칭적인 종 모양 분포 | 사람 키, 시험 점수 |
| 지수 분포 | 특정 사건이 발생할 때까지 걸리는 시간 | 택시 도착 시간 |
| 감마 분포 | 여러 번의 지수 분포를 합친 형태 | 3번째 고객이 도착할 때까지 걸리는 시간 |
3. 분포의 시각적 이해
1) 정규 분포 (Bell Curve)
- 데이터가 평균을 중심으로 대칭적인 종 모양을 이루는 가장 대표적인 분포
- 예) 시험 점수, 키, 몸무게 등
2) 이항 분포 (Binomial Distribution)
- 성공/실패가 있는 실험을 여러 번 수행할 때 성공 횟수의 분포
- 예) 동전을 10번 던졌을 때 앞면이 나오는 횟수
3) 포아송 분포 (Poisson Distribution)
- 일정 시간 동안 발생하는 사건의 빈도 수를 예측하는 분포
- 예) 1시간 동안 카페에 방문하는 고객 수
4. 분포를 왜 사용할까?
- 데이터 패턴을 이해할 수 있음
- 데이터가 어떻게 퍼져 있는지 알면 분석이 쉬워짐
- 미래 예측 가능
- 특정 분포를 따르면 미래 데이터를 예측할 수 있음
- 통계적 검정을 수행할 수 있음
- 데이터가 특정 분포를 따른다고 가정하고 검정 수행 가능
5. 결론
- *분포(Distribution)**는 데이터가 특정 값 주변에서 어떻게 퍼져 있는지를 나타내는 개념
- 이산형 분포와 연속형 분포로 나뉨
- 정규 분포, 이항 분포, 포아송 분포, 지수 분포 등 다양한 유형이 있음
- 데이터를 분석하고 예측할 때 반드시 고려해야 하는 핵심 개념
웹사이트에서 체류분포, 연속형 데이터, 이산형 데이터
확률 질량 함수 (Probability Mass Function, PMF):
이산 확률 변수의 분포를 나타내는 함수로, 각 값에서의 함수 값 자체가 확률을 의미합니다. PDF와는 달리 이산형 데이터에 사용됩니다. (예: 동전 던지기, 주사위 굴리기)에서 특정한 결과가 나올 확률을 나타내는 수식
확률 질량 함수(PMF)는 이산형 확률 분포에서 특정한 값이 나올 확률을 계산하는 함수입니다.
쉽게 말해, 이산형 데이터(예: 동전 던지기, 주사위 굴리기)에서 특정한 결과가 나올 확률을 나타내는 수식입니다.
1. PMF의 특징
- 이산형 확률 분포에서만 사용됨 (즉, 연속적인 값이 아닌 개별적인 값)
- 각 값이 나올 확률을 명확하게 정의함
- 모든 확률을 더하면 1이 됨
2. PMF 예제
1) 동전 던지기 (베르누이 분포)
- 동전을 던졌을 때 앞면(1)이 나올 확률 = 0.5, 뒷면(0)이 나올 확률 = 0.5
- PMF로 표현하면 다음과 같음 P(X=x)={0.5,0.5,if x=0 (뒷면)if x=1 (앞면)
- P(X=x)={0.5,if x=0 (뒷면)0.5,if x=1 (앞면)P(X = x) = \begin{cases} 0.5, & \text{if } x = 0 \text{ (뒷면)} \\ 0.5, & \text{if } x = 1 \text{ (앞면)} \end{cases}
2) 주사위 굴리기
- 1부터 6까지 숫자가 나올 확률은 모두 동일한 1/61/61/6
- PMF로 표현하면 P(X=x)={1/6,0,if x=1,2,3,4,5,6otherwise
- P(X=x)={1/6,if x=1,2,3,4,5,60,otherwiseP(X = x) = \begin{cases} 1/6, & \text{if } x = 1, 2, 3, 4, 5, 6 \\ 0, & \text{otherwise} \end{cases}
3. PMF 그래프
각 확률을 시각적으로 나타내면 막대 그래프 형태가 됨.
예를 들어, 주사위 확률 분포를 그리면 1부터 6까지 각각 1/61/61/6의 높이를 가진 막대 그래프가 됨.
4. PMF vs. PDF
구분 확률 질량 함수 (PMF) 확률 밀도 함수 (PDF)
| 사용 대상 | 이산형 변수 (정수 값) | 연속형 변수 (실수 값) |
| 예시 | 주사위, 동전 던지기 | 키, 몸무게, 온도 |
| 그래프 | 막대 그래프 형태 | 곡선 형태 |
5. 결론
- PMF는 이산형 확률 분포에서 특정 값이 나올 확률을 계산하는 함수
- 동전 던지기, 주사위 굴리기, 이항 분포 등에서 사용됨
- 확률을 시각화하면 막대 그래프 형태로 나타남
- PMF는 이산형 변수, PDF는 연속형 변수에 사용됨
확률 밀도 함수(PDF) :
확률의 분포를 보는것 연속형 확률 변수 X의 분포를 나타내는 함수
PDF의 값 자체는 확률이 아니며, 항상 음이 아닌 값을 가집니다
확률 밀도 함수(PDF)는 연속형 확률 분포에서 특정한 값 근처에서 나타날 확률을 나타내는 함수입니다.
쉽게 말해, 연속적인 값(예: 키, 몸무게, 온도 등)에서 특정 구간에 데이터가 얼마나 분포하는지를 나타내는 곡선입니다.
1. PDF의 특징
- 연속형 확률 변수에서 사용됨 (정확한 하나의 값이 아닌 특정 구간의 확률을 계산)
- 확률의 개념이 "특정 값"이 아니라 "범위"에서 얼마나 많이 나타나는가로 바뀜
- 특정 값 하나의 확률은 0이지만, 범위 내 확률을 계산할 수 있음
- 확률을 구하려면 적분(면적 계산)을 해야 함P(a≤X≤b)=∫abf(x)dx 즉, 특정 구간에서의 확률은 PDF 곡선 아래의 면적으로 표현됨
- P(a≤X≤b)=∫abf(x)dxP(a \leq X \leq b) = \int_{a}^{b} f(x) dx
2. PDF 예제
1) 정규 분포 (Normal Distribution)
- 평균을 중심으로 대칭적인 종 모양(Bell Shape)의 곡선을 가짐
- 예) 시험 점수, 사람 키, 몸무게 등f(x)=2πσ21e−2σ2(x−μ)2
- μ\muμ : 평균
- σ\sigmaσ : 표준편차
- f(x)=12πσ2e−(x−μ)22σ2f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}
- 특정 점 X=170X = 170X=170에서 확률을 구하는 것이 아니라, **"165cm ~ 175cm 사이에 있을 확률"**을 구함.
2) 지수 분포 (Exponential Distribution)
- 특정 사건이 발생할 때까지의 시간을 모델링하는 분포
- 예) 택시가 도착하는 시간, 고객이 줄을 서서 기다리는 시간f(x)=λe−λx,x≥0
- λ\lambdaλ : 사건이 발생하는 평균 비율
- f(x)=λe−λx,x≥0f(x) = \lambda e^{-\lambda x}, \quad x \geq 0
3. PDF 그래프
PDF는 연속적인 값을 가지므로 곡선 형태로 나타남.
예를 들어, 정규 분포의 PDF는 중앙(평균)에서 가장 높고, 양쪽으로 점점 낮아지는 종 모양을 가짐.
4. PDF vs. PMF
구분 확률 밀도 함수 (PDF) 확률 질량 함수 (PMF)
| 사용 대상 | 연속형 변수 (실수 값) | 이산형 변수 (정수 값) |
| 예시 | 키, 몸무게, 온도 | 주사위, 동전 던지기 |
| 그래프 | 곡선 형태 | 막대 그래프 형태 |
| 확률 계산 | 특정 범위 확률은 적분으로 구함 | 특정 값의 확률을 직접 구함 |
5. 결론
- PDF는 연속형 확률 변수에서 특정 구간에서 값이 나타날 확률을 나타내는 함수
- 특정 값의 확률은 0이지만, 특정 범위(예: 165cm~175cm)에서의 확률을 구할 수 있음
- 정규 분포, 지수 분포 등의 연속 확률 분포에서 사용됨
- PMF는 개별적인 값(이산형), PDF는 연속적인 값에서 사용됨
누적 분포 함수 (Cumulative Distribution Function, CDF):
확률 변수의 값이 특정 값 이하가 될 확률을 나타내는 함수로, 연속형 및 이산형 모두에 사용됩니다. CDF는 PDF를 적분하여 얻을 수 있으며, 반대로 PDF는 CDF를 미분하여 구할 수 있습니다.
누적 분포 함수(CDF)는 특정 값 이하의 확률을 나타내는 함수입니다.
즉, **"어떤 값 X 이하의 확률은 얼마인가?"**를 계산할 때 사용됩니다.
1. CDF의 정의
누적 분포 함수(CDF) F(x)F(x)F(x)는 확률 변수 XXX가 특정 값 xxx 이하일 확률을 의미하며, 수식으로 표현하면 다음과 같습니다.
F(x)=P(X≤x)F(x) = P(X \leq x)
F(x)=P(X≤x)
즉, CDF는 특정 값까지의 확률을 누적해서 더한 값입니다.
- 이산형 확률 변수에서 CDFF(x)=k=−∞∑xP(X=k)주어진 xxx 이하의 모든 PMF 값을 더한 것.
- F(x)=∑k=−∞xP(X=k)F(x) = \sum_{k=-\infty}^{x} P(X = k)
- 연속형 확률 변수에서 CDFF(x)=∫−∞xf(t)dtPDF(확률 밀도 함수)를 적분하여 특정 값까지의 확률을 구한 것.
- F(x)=∫−∞xf(t)dtF(x) = \int_{-\infty}^{x} f(t) dt
2. CDF 예제
1) 주사위 굴리기 (이산형 CDF)
- 주사위를 던질 때, X가 나올 수 있는 값: {1, 2, 3, 4, 5, 6}
- XX
- 특정 값 이하의 확률을 구함:
- P(X≤3)=P(X=1)+P(X=2)+P(X=3)=16+16+16=0.5P(X \leq 3) = P(X=1) + P(X=2) + P(X=3) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = 0.5P(X≤3)=P(X=1)+P(X=2)+P(X=3)=61+61+61=0.5
- 즉, 주사위를 던졌을 때 1, 2, 3 중 하나가 나올 확률 = 50%
2) 정규 분포 (연속형 CDF)
- 평균 170cm, 표준편차 5cm인 키 데이터를 가정
- P(X≤175)P(X \leq 175)P(X≤175) = "키가 175cm 이하일 확률은?"
- 정규 분포의 CDF를 사용하면, 해당 값을 구할 수 있음.
3. CDF 그래프
- CDF 그래프는 항상 0에서 시작하여 1(100%)에 도달하는 형태
- 값이 증가할수록 확률이 누적되므로 계단형(이산형) 또는 S자 곡선(연속형) 형태
4. CDF vs. PDF vs. PMF
구분 누적 분포 함수 (CDF) 확률 밀도 함수 (PDF) 확률 질량 함수 (PMF)
| 사용 대상 | 이산형 & 연속형 변수 | 연속형 변수 | 이산형 변수 |
| 의미 | 특정 값 이하의 확률 | 특정 값 주변에서 나타날 확률 | 특정 값 하나의 확률 |
| 그래프 | 0에서 1까지 증가 | 곡선 형태 | 막대 그래프 |
5. 결론
- CDF는 특정 값 이하의 확률을 나타내는 함수
- PMF(PMF 값의 누적), PDF(적분)에서 확률을 누적한 것
- S자 형태(연속형) 또는 계단형(이산형) 그래프를 가짐
- 확률이 0에서 시작하여 1(100%)까지 증가함
- 데이터 분석, 확률 계산, 누적 확률 예측 등에 활용됨
"확률 분포 함수"나 "밀도 함수"라는 용어가 가끔 혼용되기도 하지만, 이는 문맥에 따라 PDF나 PMF를 지칭할 수 있으므로 주의가 필요
이산형 확률분포
이산형 확률분포는 가질 수 있는 값이 특정한 개별적인 값(정수)으로 이루어진 확률 분포입니다.
즉, 연속적인 값이 아니라, 특정한 개별 값들에 대해 확률이 정의되는 분포입니다.
1. 이산형 확률분포의 특징
- 변수가 가질 수 있는 값이 연속적이지 않고, 개별적인 정수 값
- PMF(확률 질량 함수, Probability Mass Function)를 사용하여 확률을 계산
- 확률의 총합은 항상 1(100%)
- 이산형 변수를 가짐 (예: 주사위 숫자, 동전 앞뒤, 고객 방문 횟수)
2. 대표적인 이산형 확률분포
1) 베르누이 분포 (Bernoulli Distribution)
- 성공(1) 또는 실패(0)만 존재하는 실험
- 예) 동전 던지기(앞면=1, 뒷면=0), 맞춤법 검사(맞음=1, 틀림=0)
P(X=x)={p, if x=1 1−p, if x=0
- ppp = 성공 확률, 1−p = 실패 확률
- 1−p1-p
2) 이항 분포 (Binomial Distribution)
- 베르누이 실험을 여러 번 반복할 때 성공 횟수를 따르는 분포
- 예) 10번 동전을 던졌을 때 앞면이 나오는 횟수
- 확률 공식:
- n = 전체 시행 횟수
- k = 성공 횟수
- p = 성공 확률
- λ = 단위 시간당 평균 발생 횟수
- k = 특정 횟수
3. 이산형 확률분포 vs 연속형 확률분포
구분 이산형 확률분포 연속형 확률분포
| 값의 형태 | 개별적인 정수 값 | 연속적인 실수 값 |
| 예시 | 동전 앞뒤, 주사위 값, 고객 방문 횟수 | 키, 몸무게, 온도, 시간 |
| 확률 함수 | 확률 질량 함수(PMF) | 확률 밀도 함수(PDF) |
| 확률 계산 | 특정 값의 확률을 직접 계산 | 특정 범위 내 확률을 적분 계산 |
4. 결론
- 이산형 확률분포는 개별적인 정수 값에서 확률을 계산하는 분포
- PMF(확률 질량 함수)를 사용하여 확률을 구함
- 베르누이, 이항, 포아송 분포 등이 대표적인 예시
- 연속형 확률분포와 비교하여 특정한 개별 값에서 확률을 직접 계산할 수 있음
3) 포아송 분포 (Poisson Distribution)
포아송(Poisson)은 특정한 의미를 가진 단어가 아니라, 이 확률 분포를 연구한 수학자의 이름에서 유래
"어떤 기간 동안 사건이 몇 번 일어날까?", "특정 공간 안에서 사건이 몇 번 발생할까?" 등 랜덤하게 발생하는 사건의 개수를 예측할 때 활용하는 분포
- 특정 시간(또는 공간) 동안 사건이 몇 번 발생할지를 나타내는 분포
- 예) 1시간 동안 고객이 몇 명 방문할까?, 1km 도로에 차량 사고가 몇 건 발생할까?
포아송 분포는 어떤 사건이 일정한 시간이나 공간 안에서 몇 번 발생하는지를 나타내는 확률 분포입니다.
1. 언제 사용하나요?
- 특정 시간 동안 발생하는 사건의 개수를 예측할 때
- 특정 공간 내에서 이벤트가 몇 번 발생하는지 분석할 때
2. 예제
✔ 1시간 동안 카페에 손님이 몇 명 올까?
✔ 1km 도로에서 교통사고가 몇 번 발생할까?
✔ 1년 동안 특정 질병에 걸리는 환자가 몇 명일까?
이처럼 랜덤하게 발생하는 사건의 개수를 분석할 때 사용됩니다.
3. 공식
- kkk = 사건이 발생한 횟수 (예: 1시간 동안 온 손님 수)
- λ\lambdaλ = 평균적으로 발생하는 횟수 (예: 1시간 동안 평균 10명 방문)
- eee = 약 2.718 (자연상수)
4. 핵심 포인트
✔ 랜덤하게 발생하는 사건의 개수를 예측하는 분포
✔ 평균 발생 횟수(λ)만 알면 확률을 계산할 수 있음
✔ 시간, 공간에 따라 이벤트가 발생하는 경우에 적합
5. 결론
"어떤 사건이 일정한 시간이나 공간 안에서 몇 번 발생할지를 계산하는 확률 분포"
예: 카페 손님 수, 교통사고 횟수, 병원 환자 수 예측 등에 사용
베르누이 분포 (Bernoulli Distribution)
시행이 성공과 실패와 같은 두 가지 결과만 가지는 실험의 확률
두 가지 결과만 가능: 일반적으로 1(성공) 또는 0(실패)로 표시
- 동전 던지기 (앞/뒤)
- 주사위 던지기(6이 나올 경우(성공), 6이 아닌 수가 나올 경우(실패))
- 제품 불량 여부 (정상/불량)
- 웹사이트 방문자가 광고를 클릭할지 여부
- 구직자가 면접에 합격할지 여부 (합격/불합격)
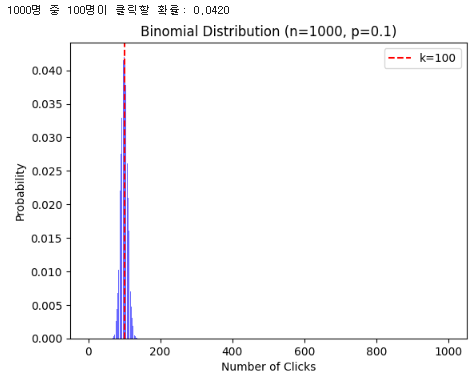
이항분포 (Binomial Distribution)
어떤 일이 여러 번 일어날 때, 특정한 결과가 몇 번 일어날 확률을 구하는 방법이에요. 매 시행마다 일어날 확률이 동일할 경우 사용.
- 베르누이 분포: 한 번의 시행 (동전 한 번 던지기)
- 이항 분포: n번의 시행에서 성공 횟수 (동전 10번 던져서 앞면이 나온 횟수)
기하분포 (Geometric Distribution)
성공 확률이 p인 베르누이 시행에서, 처음으로 성공이 발생할 때까지 필요한 시행 횟수의 확률 분포
"처음 성공할 때까지 몇 번 시행해야 하는가?"를 분석하는 확률 분포
예: 동전 던지기, 고객 응답, 스포츠 경기 등에서 사용
음이항분포 (Negative Binomial Distribution)
'음이항(Negative Binomial)'이라는 용어는 이항(Binomial) 분포와의 관계에서 유래
성공 확률이 p인 베르누이 시행에서, 정확히 r번의 성공을 달성하기 위해 필요한 시행 횟수에 대한 확률 분포
"r번째 성공이 나올 때까지 몇 번 시행해야 하는가?"를 분석하는 확률 분포
예: 농구 슛, 고객 응답, 기계 고장 예측 등에서 사용.
σ(소문자 시그마) vs. Σ(대문자 시그마)
그리스 문자 **시그마(Sigma, Σ, σ)**는 수학과 통계에서 자주 사용되지만, **대문자(Σ)와 소문자(σ)**는 각각 다른 의미
1. 대문자 시그마 (Σ)
▶ 용도: 합(Summation, 시그마 기호)
- Σ는 수학에서 합을 나타내는 기호로 사용된다.
- 여러 개의 항을 더하는 연산(시그마 합산, summation)에서 사용된다.
예제
∑i=15i=1+2+3+4+5=15\sum_{i=1}^{5} i = 1 + 2 + 3 + 4 + 5 = 15
- Σ 기호 아래(i=1): 시작 값(1)
- Σ 기호 위(5): 종료 값(5)
- i: 더할 대상
2. 소문자 시그마 (σ)
▶ 용도: 통계에서 표준 편차(Standard Deviation)
- σ는 데이터의 산포(퍼짐 정도)를 측정하는 표준 편차를 나타냄
- 정규 분포에서 데이터가 평균(μ) 주변에 얼마나 퍼져 있는지를 표현
공식
σ=∑(xi−μ)2N\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}
- xix_i: 개별 데이터 값
- μ\mu: 평균
- NN: 전체 데이터 개수
- ∑\sum: (대문자 시그마) 합을 의미
표준 편차의 의미
- σ(시그마)가 작을수록 데이터가 평균(μ) 근처에 집중됨
- σ(시그마)가 클수록 데이터가 넓게 퍼짐
3. 두 개의 차이 요약
| 구분 | 대문자 시그마 (Σ) | 소문자 시그마 (σ) |
| 의미 | 합(Σummation) | 표준 편차(Standard Deviation) |
| 사용 분야 | 수학, 확률, 통계 | 통계, 확률 |
| 역할 | 여러 개의 값을 더하는 기호 | 데이터의 변동성을 측정하는 값 |
| 예제 | ∑i=1ni=1+2+...+n\sum_{i=1}^{n} i = 1 + 2 + ... + n∑i=1ni=1+2+...+n | σ=∑(xi−μ)2N\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}σ=N∑(xi−μ)2 |
4. 정리
- Σ (대문자 시그마): "합을 구할 때" 사용
→ 여러 개의 수를 더하는 연산 기호 - σ (소문자 시그마): "데이터의 변동성을 나타낼 때" 사용
→ 표준 편차를 의미하며 데이터가 평균에서 얼마나 퍼져 있는지 측정
즉, Σ(시그마)는 덧셈 기호, **σ(시그마)는 통계 개념(표준 편차)**으로 이해하면 된다.
연속형 확률분포
정규분포 (Normal Distribution, Gaussian Distribution)
평균 근처의 값이 가장 자주 발생하고, 양쪽으로 갈수록 발생 확률이 낮아지는 형태의 분포
A. 표준편차는 "숫자"이고, 정규분포는 "그래프"이다 .B. 표준편차는 정규분포의 폭을 결정하는 요소이다.
C. 표준편차는 다양한 분포에서 사용 가능하다.
표준편차는 숫자(σ)이고, 정규분포는 그래프(Bell Shape)이다. 표준편차는 정규분포의 폭을 결정하는 요소일 뿐, 정규분포 자체는 아니다. 표준편차는 모든 분포에서 계산할 수 있지만, 정규분포는 특정한 확률분포를 의미 |
표준 정규분포
평균이 0이고 분산이 1인 정규분포
지수분포
한 번의 사건이 발생할 때까지의 시간
균등분포 (Uniform Distribution)
모든 구간이 동일한 확률을 가지는 연속형 분포
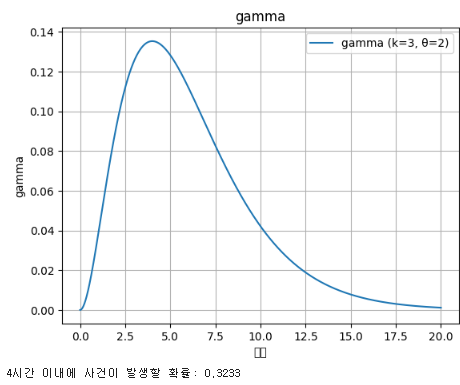
감마분포 (Gamma Distribution)
지수분포가 합쳐진 형태로, 특정 횟수의 사건 발생까지 걸리는 시간
연속형 분포 : 정류분포, 지수분포, 균등분포
코렙으로 실습하면서 익힐예정
코드작성시 주석이나 텍스트를 꼭 다는것이 좋다(같이 프로젝트 협업 등 차원에서)
import numpy as np
import matplotlib.pyplot as plt
import warnings
# 폰트 관련 경고 메시지 숨기기
warnings.filterwarnings("ignore", category=UserWarning)
import matplotlib as mpl
mpl.rcParams['font.family'] = 'sans-serif'
PMF
from scipy.stats import binom
# 이항분포
# 치킨집 예제
n = 10 # 총 방문 손님 수
p = 0.1 # 한 명이 치킨을 주문할 확률
k = 4 # 정확히 4명이 주문할 확률
# PMF 계산
prob_4_orders = binom.pmf(k, n, p)
print(f"10명 중 정확히 4명이 치킨을 주문할 확률: {prob_4_orders:.4f}")
10명 중 정확히 4명이 치킨을 주문할 확률: 0.0112
CDF와 PDF
from scipy.stats import norm
# 서비스 운영 시간 범위 (오전 11시 ~ 밤 12시) 시간기준으로 셋팅한다
time_hours = np.linspace(11, 24, 100)
# PDF: 오후 7시(19시) 피크 타임
peak_time = 19
spread = 2 # 확률 분포의 퍼짐 정도 (±2시간)
pdf_values = norm.pdf(time_hours, peak_time, spread)
# CDF: 누적 확률 계산
cdf_values = norm.cdf(time_hours, peak_time, spread)
# CDF를 조정하여 오후 7시(19시)에서 80% 도달
cdf_values = cdf_values / np.max(cdf_values) * 0.8
cdf_values[time_hours >= 19] = 0.8 + (cdf_values[time_hours >= 19] - 0.8) / (1 - 0.8) * 0.2
# PDF 그래프 그리기 회사에서 시간대별로 분포보는걸로 가장 많이 본다.
plt.figure(figsize=(6, 4))
plt.plot(time_hours, pdf_values, label="Probability Density Function (PDF)", color='blue')
plt.axvline(19, color='red', linestyle='--', label="Peak time (7 PM)") # 피크 시간 표시
plt.xlabel("Time (Hour)") # x축: 시간 (시)
plt.ylabel("Probability Density") # y축: 확률 밀도
plt.title("Chicken Restaurant Customer Probability (PDF)") # 그래프 제목
plt.legend()
plt.show()
# CDF 개별 그래프 그리기
plt.figure(figsize=(6, 4))
plt.plot(time_hours, cdf_values, label="Cumulative Distribution Function (CDF)", color='green')
plt.axvline(19, color='red', linestyle='--', label="80% Customers Arrived by 7 PM") # 80% 도달 시점 표시
plt.xlabel("Time (Hour)") # x축: 시간 (시)
plt.ylabel("Cumulative Probability") # y축: 누적 확률
plt.title("Chicken Restaurant Customer Cumulative Probability (CDF)") # 그래프 제목
plt.legend()
plt.show()
베르누이 분포
from scipy.stats import bernoulli
# 성공 확률 p
p = 0.7
# 데이터 생성
x = [0, 1]
y = bernoulli.pmf(x, p)
# 그래프 그리기
plt.bar(x, y, tick_label=['f (0)', 't (1)'])
plt.title(f'bernoulli (p={p})')
plt.xlabel('result')
plt.ylabel('bernoulli')
plt.show()
# 성공 확률과 실패 확률 출력
print(f"성공 확률: {p}")
print(f"실패 확률: {1 - p}")
이항분포
from scipy.stats import binom
# 문제7 시행에 8번 성공할 확률, P=0.4
# 시행 횟수 n, 성공 확률 p
n = 8
p = 0.4
# 이항분포 데이터 생성
x = np.arange(0, n+1)
y = binom.pmf(x, n, p)
# 확률 분포 그래프 그리기
plt.bar(x, y, color='blue', alpha=0.6)
plt.title(f'Binomial Distribution (n={n}, p={p})')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# 특정 성공 횟수의 확률 계산 (8번 성공할 확률)
k = 8
prob = binom.pmf(k, n, p)
print(f"Probability of {k} successes out of {n} trials: {prob:.4f}")
# 이메일 클릭 확률
p = 0.1 # 성공 확률 (이메일 클릭 확률)
n = 1000 # 이메일을 보낸 고객 수
k = 100 # 클릭할 고객 수
# 700명이 클릭할 확률 계산
prob_5_clicks = binom.pmf(k, n, p)
print(f"1000명 중 100명이 클릭할 확률: {prob_5_clicks:.4f}")
# 확률 분포 그래프 그리기
x = np.arange(0, n+1)
y = binom.pmf(x, n, p)
plt.bar(x, y, color='blue', alpha=0.6)
plt.axvline(k, color='red', linestyle='dashed', label=f'k={k}')
plt.title(f'Binomial Distribution (n={n}, p={p})')
plt.xlabel('Number of Clicks')
plt.ylabel('Probability')
plt.legend()
plt.show()
기하분포
from scipy.stats import geom
# 성공 확률 p
p = 0.5
# 기하분포 데이터 생성
x = np.arange(1, 15) #1부터 14까지
y = geom.pmf(x, p) #각 시행 횟수에 대한 확률 질량 함수 계산
# 그래프 시각화
plt.bar(x, y)
plt.title(f'geom (p={p})')
plt.xlabel('시행 횟수')
plt.ylabel('확률')
plt.show()
# 특정 시행 횟수 확률 (예: 6번째 시도에서 성공할 확률)
k = 6
prob = geom.pmf(k, p)
print(f"{k}번째 시도에서 성공할 확률: {prob:.4f}")
음이항분포
from scipy.stats import nbinom
# 성공 횟수 r, 성공 확률 p
r = 3 # 목표 구매 횟수
p = 0.3 # 방문당 구매 확률
# 음이항분포 데이터 생성
x = np.arange(0, 30)
y = nbinom.pmf(x, r, p)
# 그래프 그리기
plt.bar(x, y)
plt.title(f'nbinom (r={r}, p={p})')
plt.xlabel('failure')
plt.ylabel('nbinom')
plt.show()
# 특정 실패 횟수 확률 (예:K 5번 방문 후 r 3번째 구매 성공)
k = 5
prob = nbinom.pmf(k, r, p)
print(f"{k}번째 방문에서 {r}번째 구매 성공할 확률: {prob:.4f}")
포아송분포
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
# 평균 도착률 (시간당 평균 15건의 문의가 옴)
lambda_ = 15
# 특정 시간대에 25건 이상 문의가 올 확률 (P(X ≥ 25))
prob_25_or_more = 1 - stats.poisson.cdf(24, lambda_)
print(f"특정 시간대에 문의가 15건 이상 올 확률: {prob_25_or_more:.4f}")
# 포아송 분포 확률 질량 함수 (PMF) 계산 lambda 값이 30이상일때 정규분포처럼 된다.
x = np.arange(0, 40) # 0건 ~ 40건 범위
y = stats.poisson.pmf(x, lambda_)
# 그래프 그리기
plt.figure(figsize=(8, 5))
plt.bar(x, y, color='blue', alpha=0.6, label="Poisson PMF")
# 15건 이상 구간 강조 (확률 부분 색 다르게)
plt.bar(x[x >= 15], y[x >= 15], color='red', alpha=0.6, label="P(X ≥ 15)")
# 그래프 제목 및 라벨 설정
plt.xlabel("Number of Inquiries") # x축: 문의 건수
plt.ylabel("Probability") # y축: 확률
plt.title(f"Poisson Distribution (λ={lambda_})") # 제목
plt.legend()
plt.show()
정규분포
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 평균과 표준편차
mu = 0
sigma = 1
# 정규분포 데이터 생성
x = np.linspace(-5, 5, 1000)
y = norm.pdf(x, mu, sigma)
# 그래프 그리기
plt.plot(x, y, label=f'Normal Distribution ($\mu={mu}$, $\sigma={sigma}$)')
plt.title('Normal Distribution')
plt.xlabel('x')
plt.ylabel('Normal Distribution')
plt.legend()
plt.grid()
plt.show()
# 특정 구간에 있을 확률 계산 (예: -1 < x < 1)
prob = norm.cdf(1, mu, sigma) - norm.cdf(-1, mu, sigma)
print(f"-1과 1 사이에 위치할 확률: {prob:.4f}")
균등분포
from scipy.stats import uniform
# 균등분포 구간
a = 3 # 최소값
b = 6 # 최대값
# 균등분포 데이터 생성
x = np.linspace(a - 1, b + 1, 1000)
y = uniform.pdf(x, a, b - a)
# 그래프 그리기
plt.plot(x, y, label=f'uniform U({a}, {b})')
plt.title('uniform')
plt.xlabel('x')
plt.ylabel('uniform')
plt.legend()
plt.grid()
plt.show()
# 특정 구간 확률 계산 (예: 3 < x < 6)
prob = uniform.cdf(6, a, b - a) - uniform.cdf(3, a, b - a)
print(f"3와 6 사이에 위치할 확률: {prob:.4f}")
감마분포
from scipy.stats import gamma
# 감마분포 파라미터 (독립적인사건이 여러번 발생했다)
k = 3 # 형태 모수 (사건 횟수)
theta = 2 # 척도 모수
# 감마분포 데이터 생성
x = np.linspace(0, 20, 1000)
y = gamma.pdf(x, a=k, scale=theta)
# 그래프 그리기
plt.plot(x, y, label=f'gamma (k={k}, θ={theta})')
plt.title('gamma')
plt.xlabel('시간')
plt.ylabel('gamma')
plt.legend()
plt.grid()
plt.show()
# 특정 시간 이하일 확률 (예: 4시간 이내에 사건 발생 확률)
prob = gamma.cdf(4, a=k, scale=theta)
print(f"4시간 이내에 사건이 발생할 확률: {prob:.4f}")
'데이터 분석가:Applied Data Analytics' 카테고리의 다른 글
| 데이터 분석 용어 및 정의 (영문)/(한글) (1) | 2025.03.05 |
|---|---|
| 올라운드 프로패셔널에 대하여 (3) | 2025.03.05 |
| 빅분기(빅데이터 분석기사) 시험이란? (0) | 2025.03.04 |
| Zotero란? (1) | 2025.03.04 |
| OneTab 설치 (0) | 2025.03.03 |