확률과 분포 이해하기 2]

중심 극한 정리(CLT)란? 

중심 극한 정리(Central Limit Theorem, CLT)는 통계학에서 가장 기본적이고 중요한 정리로, 다음과 같이 정의: 독립적이고 동일한 분포(i.i.d.)를 가진 확률 변수들의 표본 평균은 표본의 크기가 충분히 커질 때 정규 분포에 근사하게 된다는 정리. 중심 극한 정리의 핵심 내용 모집단의 분포와 무관: 원래 모집단이 어떤 분포를 따르든 상관없이 적용됩니다. 표본 크기: 일반적으로 표본 크기(n)가 30 이상이면 충분히 크다고 간주합니다. 표본 평균의 분포: 표본 평균은 평균이 μ(모집단의 평균)이고 표준편차가 σ/√n(모집단의 표준편차/√표본크기)인 정규분포에 근사합니다. 중심 극한 정리의 조건 확률 변수들이 서로 독립적이어야 함 동일한 확률 분포를 가져야 함 확률 분포의 기댓값(μ)과 표준편차(σ)가 유한해야 함. 중심 극한 정리의 중요성 중심 극한 정리가 중요한 이유는 다음과 같습니다: 통계적 추론의 기반: 표본 통계량을 이용해 모수를 추정할 수 있는 수학적 근거를 제공합니다. 모집단 분포 무관: 모집단의 분포 형태에 상관없이 표본 평균의 분포가 정규분포에 근사한다는 점에서 통계적 분석에 큰 편의성을 제공합니다. 실용적 응용: 품질관리, 식스 시그마 등 다양한 분야에서 활용됩니다. 대규모 데이터 분석: 대규모 데이터셋에서의 통계적 분석과 추론을 안정적으로 수행할 수 있게 해줍니다. 중심 극한 정리는 모집단을 직접 확인할 수 없는 실제 세계에서 표본을 통해 모집단의 특성을 추론하는 데 필수적인 이론적 기반을 제공합니다

공정관리에서 필수로 나오는 몬테카를로 법칙과 비교해 봤습니다.

중심 극한 정리(CLT)와 몬테카를로 시뮬레이션은 통계학과 확률에 관련된 개념이지만 그 본질과 용도가 다르다. 기본 개념 비교 중심 극한 정리(CLT)는 독립적이고 동일한 분포를 가진 확률 변수들의 표본 평균이 표본 크기가 충분히 커질 때 정규 분포에 근사한다는 수학적 정리. 이는 모집단의 분포 형태와 무관하게 적용. 몬테카를로 시뮬레이션은 무작위 샘플링을 반복적으로 사용하여 결과의 확률 분포를 추정하는 계산 알고리즘입니다. 이는 불확실성이 있는 시스템의 다양한 결과 가능성을 모델링하는 방법입니다. 모나코를 구성하는 열 개의 행정구 중 하나. 거주 인구 약 3천명에 프랑스, 이탈리아와 매우 근접한 위치로, 수도 모나코 시와는 항구를 끼고 반대쪽에 위치한다. 당시 모나코 공인 샤를 3세가 도박장 건설을 허가하면서 유명 관광지 및 유흥지로 성장하는 계기가 되었다. 도박장 외에도 라보토 해변이 있는 북부 해변가, 그리고 해외 유명 제품들을 다루는 시장인 몬테카를로 거리로도 유명한 곳이다. 프랑스어로는 Monte-Carlo, 모나코어로는 Monte-Carlu, 오크어로는 Montcarles라고 한다. 카지노 및 도박으로 유명하고, 포뮬러 1의 유명 서킷 모나코 서킷이 위치하며, 동시에 WRC의 매년 첫번째 개최지이기도 하다. 대프니 뒤 모리에의 소설과 앨프리드 히치콕의 영화 (그리고 뮤지컬) 레베카에서 주인공 막심(Maxim de Winter)이 나를 만난 곳이 몬테카를로이다. 동명의 카지노에서 이름을 따온, 무작위로 추출된 난수를 이용하여 함수의 값을 계산하는 통계학의 방법. 최적화, 수치적분, 확률분포로부터의 추출 등에 쓰인다. 몬테 카를로란 이름이 붙은 이유는 이 방법이 알려지게 된 연구가 바로 로스 알라모 과학 연구소의 핵무기 개발 연구였기 때문이다. 해당 연구에는 스타니스와프 울람(Stanislaw Ulam)이존 폰 노이만과 함께 이 새로운 수치 해석 방법을 만들고 있었다. 핵무기 연구는 극비사항이라서 코드명이 필요했는데, 울람의 동료였던니콜라스 메트로폴리스가 울람의 삼촌이 친척들에게 돈을 빌려서 자주 가던 카지노의 이름을 코드명으로 추천했고, 그것이 받아들여진 것이다. 몬테 카를로 방법은 맨해튼 계획으로원자폭탄을 성공적으로 개발하고 난 뒤,수소폭탄개발 계획을 세울 때 고안된 것이다. 이 당시에제2차 세계 대전은 이미 끝났고 끝내주는 위력을 가진 원자폭탄도 확보했는데, 또 막대한 예산을 들여 수소폭탄을 개발하려니까 일단핵융합을 실제로 일으킬 수 있는지부터 확인해 볼 필요가 있었다. 그런데 당연히 아직 수소폭탄 제조를 위한 참고 자료가 없었기 때문에, 이것을 확인하기 위해서는 일단 많은 돈이 들어가는 실험부터 해야 한다는딜레마에 빠지게 되었다. 그래서 1946년에 예산을 타내기 위해 당시 막 등장한 컴퓨터를 사용해서 간단한 (하지만 당시로는 복잡한) 시뮬레이션을 돌려봤는데, 이 때 사용한 알고리즘이 바로 몬테 카를로 방법이다.[2]참고로 몬테 카를로 방법은 컨셉 디자인이 말이 되는지 확인하는데만 사용되었고, 컨셉 디자인이 통과된 이후에 실제 수소폭탄 설계와 제작은 '엄청난 수의 연구원과 많은 예산을 갈아넣어서 될 때까지 만들어 본다'는 전통적인공밀레방식으로 수행되었다. 실험 없이 오직 컴퓨터 시뮬레이션만으로 수소폭탄을 설계하는 것은 2010년대 후반의 세계 최상급의 슈퍼 컴퓨터를 써도 불가능하다. 몬테 카를로 방법의 활용이 가장 알려진 분야는 인공지능이다. 대표적으로 알려진,구글 딥마인드의 바둑 AI알파고는 몬테 카를로 트리 탐색 (Monte Carlo Tree Search) 알고리즘이 적용됐다. 확률을 기반으로 하는 시뮬레이션은 거의 대부분 마르코프 체인 몬테 카를로 방법을 사용한다고 해도 과언이 아니다. 특히베이즈 확률론과베이즈 정리를 기반으로 두는 통계학의 흐름인 '베이즈 통계학'은 실제 활용을 해야 하는 상황에서는 계산의 복잡도가 높아, 이 MCMC 방법이 없었으면 도저히 발전하지 못했을 것이라 말할 정도로 해당 기법에 많이 의존하고 있다. 핵 및 입자물리학에서도 광범위하게 활용된다. 여기서는 난수 하나를 만드는 게 아니라 아예 충돌 이벤트 자체를 만든다. 예를 들어 LHC에서의 충돌 실험에서 검출된 전자들의 에너지를 모아다 그 분포를 보고 싶다고 하자. 이 분포에 대한 이론적 예측과 실험과의 비교가 필요할텐데, 사실 입자물리에서 어떤 이론적 예측을 계산하는 건 결코 쉬운 일이 아니다. 입자가 두세 개 생성되는 거면 모를까, 고에너지 충돌에서 생성되는 입자 수는 엄청나게 많다. 거기다 충돌 과정 그 자체도 굉장히 복잡하거니와 검출기 자체도 너무 복잡해서 손으로 계산할 만한 일이 절대 아니다. 이 상황에서 물리학자들은 이론적 예측을 시뮬레이션으로 해결한다. 즉 충돌이라든가 입자 간의 상호작용 및 붕괴, 검출기와의 상호작용 같은 중요한 부분들을 따로 쪼개어 이들 각각에서의 확률 분포를 계산한 다음, 이 확률들을 토대로 하여 몬테 카를로 시뮬레이션을 돌리는 것이다.[6] 말 그대로 무작위 가상 실험을 하는 것이다. 실험 한 번으로는 별 의미가 없지만 이걸 수십, 수백억 번 반복한 다음 이것들을 모아 히스토그램을 그리면 비로소 원하는 확률 분포를 얻을 수 있을 것이다. 괜히 LHC 같은 실험에서 고성능 컴퓨터가 많이 필요한 것이 아니다.[7] 이 가상 실험 결과물들을 가지고 전자들만 골라내어 그 에너지를 히스토그램으로 그린 것이 바로 우리가 원하는 이론적 예측이 되는 것이다. 그 복잡함이라든가 몬테 카를로 기법이 어떻게 쓰이는 지에 대한 자세한 내용은 LHC 문서를 참고하면 좋다. LHC만 설명했는데, 사실 대부분의 대형 실험에서는 이와 같은 방식으로 몬테 카를로 기법을 애용하다시피 한다. 아예 이론적 예측 혹은 가상 실험 결과들을 모은 걸 가지고 몬테 카를로, 아니면 MC(Monte Carlo)라고 지칭하기도 한다. 임상시험에서도 종종 활용된다. 실제로는 인간에게 할 수 없는 조작(예를 들어 암 환자를 일부러 치료를 안 하는 상황)을 MCMC로 시뮬레이션하는 경우가 많다. 허나 임상시험에서는 아무리 우량한 알고리즘으로 예측한 데이터도 실제 시험이나 후향적 관측을 통해 얻은 데이터에 비하면 가치가 떨어진다고 평가하는 경우가 많기 때문에, 차선의 방법이라 할 수 있다. 이외에도 각종 컴퓨터 시뮬레이터, 컴퓨터 게임을 개발할 때도 활용된다. (실제 플랜트 현장에서는 예상되는 공사계획을 최소만번이상 돌려봐서 수익이 남는지 손해를 보는지를 분석하기도 한다.) 현실적으로 적응하기에는 수주용으로 해보면 좋치만 안그래도 세부설계가 나오지 않은 상태에서 대략적인 계산으로 Plan을 설계하는거라 정확도 면에서는 실제 공사에 비해 떨어질수 밖에 없지만 반복적으로 돌려봄으로써 확률적으로 예측하는 프로그램이다.  물론 오라클에 프리마베라 말고 몬테라를로분석을 하는 프로그램이 별도로 있으며 금액은 프리마베라에 3~5배 금액이다. 참고로 프리마베라는 최근 금액이 500만원/개당 이다. Monte Carlo algorithm. 무작위성이 들어가는 몬테 카를로 방법을 활용한 알고리즘으로, 수행에 걸리는 시간은 확정적이지만 대신 결과물에 어떤 확률로 오차가 발생할 수 있는 알고리즘을 일컫는다. 즉 정확한 답을 보장할 수 없는 단점이 있지만, 정확한 답을 보장하는 알고리즘이 시간을 너무 많이 잡아먹거나 너무 복잡해 이용하기 어려울 경우 현실적으로 써먹기 힘들기 때문에 대신 이용하는 것이다. [출처:나무위키] 방법론 차이 중심 극한 정리: 수학적 증명에 기반한 이론적 정리 표본 평균의 분포가 정규 분포에 수렴함을 보여줌 통계적 추론의 이론적 기반 제공 몬테카를로 시뮬레이션: [출처 : 인사이트캠퍼스] 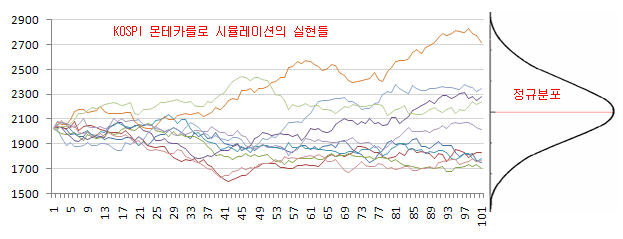반복적인 무작위 샘플링을 통한 계산 방법 일반적으로 다음 단계를 따름: 모델 구축 (수학적 모델 결정) 시뮬레이션할 변수 선택 및 확률 분포 결정 반복 시뮬레이션 실행 결과 집계 및 분석 활용 분야 중심 극한 정리: 통계적 추론 및 가설 검정 신뢰 구간 구성 표본 크기 결정 몬테카를로 시뮬레이션: 최적화 문제 수치 적분 확률 분포로부터의 샘플 생성 금융, 투자, 프로젝트 관리, 인공지능, 물리학, 공학 등 다양한 분야 핵심 차이점 목적: 중심 극한 정리는 표본 평균의 분포 특성을 설명하는 이론이고, 몬테카를로 시뮬레이션은 복잡한 시스템의 결과를 예측하는 방법입니다. 접근 방식: 중심 극한 정리는 분석적 접근이고, 몬테카를로 시뮬레이션은 계산적/수치적 접근입니다. 결과물: 중심 극한 정리는 표본 평균의 분포 특성에 대한 이론적 결론을 제공하고, 몬테카를로 시뮬레이션은 가능한 결과의 확률 분포를 생성합니다. 적용: 중심 극한 정리는 표본 통계량의 분포를 이해하는 데 사용되고, 몬테카를로 시뮬레이션은 복잡한 시스템을 모델링하고 불확실성을 평가하는 데 사용됩니다. 두 개념 모두 확률과 통계에서 중요한 역할을 하지만, 중심 극한 정리는 이론적 기반을 제공하는 반면 몬테카를로 시뮬레이션은 실제 문제 해결을 위한 계산 도구입니다.

파레토 법칙이란?

파레토 법칙(Pareto Principle)은 대부분의 결과(약 80%)가 소수의 원인(약 20%)에서 비롯된다는 통계적 원리입니다. 이 법칙은 '80:20 법칙', '중요한 소수의 법칙' 또는 '요소 희소성의 원칙'이라고도 불립니다. 파레토 법칙의 역사 이 원리는 이탈리아 경제학자 빌프레도 파레토(Vilfredo Pareto)의 이름을 따서 명명되었습니다. 1906년 파레토는 이탈리아 왕국의 토지 약 80%가 인구의 20%에 의해 소유되고 있다는 사실을 발견했습니다. 1941년, 품질 관리 컨설턴트 조셉 주란(Joseph M. Juran)이 파레토의 연구를 품질 관리와 개선 분야에 적용하면서 이 개념을 '파레토 원칙'이라고 명명했습니다. 주란은 이를 "중요한 소수와 유용한 다수"라고 표현하기도 했습니다. 파레토 법칙의 적용 사례 파레토 법칙은 다양한 분야에 적용될 수 있습니다: 비즈니스: 매출의 80%가 고객의 20%에서 발생합니다 제품 판매: 제품의 20%가 판매의 80%를 생성합니다 품질 관리: 결함의 20%가 프로세스의 80%에 영향을 미칩니다 시간 관리: 업무 시간의 20%가 결과의 80%를 생성합니다 투자: 회사 투자의 20%가 투자 이익의 80%를 생성합니다 소프트웨어: 소프트웨어 버그의 20%가 소프트웨어 오류의 80%를 유발합니다 비즈니스에서의 파레토 법칙 활용 비즈니스 분야에서 파레토 법칙은 ABC 분류법을 통해 구매를 우선순위화하는 데 사용됩니다: A등급 구매: 공급업체의 20%가 총 구매 비용의 80%를 차지합니다 B등급 구매: 공급업체의 30%가 총 구매 비용의 15%를 차지합니다 C등급 구매(테일 스펜드): 나머지 공급업체가 총 구매 비용의 5%를 차지합니다 파레토 법칙은 마케팅 ROI, 영업, 제품 제공, 수익성, 생산성 등 비즈니스의 거의 모든 측면에 영향을 미칠 수 있습니다. 파레토 법칙의 의의 파레토 법칙은 단순한 관찰에 기반한 원칙이며 과학적 법칙은 아닙니다.  정확히 80:20 비율로 적용되지 않을 수 있으며, 중요한 것은 소수의 원인이 대다수의 결과를 만든다는 불균형한 관계를 인식하는 것입니다. 이 원칙의 핵심 메시지는 정말 중요한 것에 집중함으로써 더 큰 만족이나 이익을 얻을 수 있다는 것입니다. 파레토 법칙을 따르면 자원과 에너지를 거의 이익을 가져오지 않는 활동에 낭비하지 않고 더 나은 결과를 얻을 수 있습니다 파레토 차트 (Pareto Chart) 파레토 법칙을 시각화한 대표적인 그래프는 파레토 차트입니다. 이 차트는 다음과 같은 특징을 가집니다: 참고로 파레토는 수학자이자 경제학자이자 사회학자인 등 저명한 학자여서 파레토의 이름을 따온 전문 용어가 대여섯 개에 달해 헷갈릴 수 있는데, 일반적으로 ‘파레토의 법칙’이라고 하면 이 문서의 내용을 말한다. 파레토의 이름을 딴 다른 것으로는 어느 누구에게도 손해를 주지 않으면서 누군가의 이득을 증대시키는 파레토 개선과 파레토 개선이 더 이상 불가능한 파레토 최적이 있다. 이탈리아의 경제학자 1848년 출생 1923년 사망 파리 출신 인물 [출처 : 나무위키] 세로 막대 그래프 형태로, 값들이 왼쪽에서 오른쪽으로 상대 빈도가 감소하는 순서로 표시됩니다. 주로 80%의 결과를 초래하는 상위 20%의 원인에 초점을 맞춥니다. 종종 누적 백분율을 나타내는 선 그래프가 막대 그래프와 겹쳐 표시됩니다.

파레토 법칙 과 중심 극한 정리(CLT)와의 차이점

파레토 법칙과 중심 극한 정리(CLT)는 통계학의 중요한 개념이지만 그 본질과 적용 분야가 매우 다릅니다.

기본 개념 비교

파레토 법칙(80:20 법칙)은 결과의 약 80%가 원인의 20%에서 비롯된다는 통계적 원리입니다. 이탈리아 경제학자 빌프레도 파레토가 이탈리아 토지 소유 분포를 연구하면서 발견한 법칙으로, 인구의 20%가 토지의 80%를 소유하고 있다는 사실에서 시작되었습니다.

중심 극한 정리(CLT)는 독립적이고 동일한 분포를 가진 확률 변수들의 표본 평균이 표본 크기가 충분히 커질 때 정규 분포에 근사한다는 수학적 정리입니다. 이는 원래 모집단이 어떤 분포를 따르든 상관없이 적용됩니다.

수학적 특성 비교

파레토 법칙:

• 멱법칙(power-law) 확률 분포를 따름
• 파레토 지수(α)가 1보다 클 때 유한한 평균을 가짐
• 80-20 법칙은 파레토 지수가 α ≈ 1.161일 때 정확히 성립함

중심 극한 정리:

• 표본 평균의 분포가 정규 분포에 근사함
• 모집단 분포가 유한한 분산을 가져야 함
• 표본 크기가 클수록 정규 분포에 더 가까워짐

적용 분야 비교

파레토 법칙:

• 비즈니스: 고객의 20%가 매출의 80% 창출
• 재고 관리: 제품의 20%가 이익의 80% 생성
• 시간 관리: 업무 시간의 20%가 결과의 80% 생성
• 팀 관리: 상위 20% 인재 개발에 집중

중심 극한 정리:

• 통계적 추론 및 가설 검정
• 표본 통계량의 분포 이해
• 신뢰 구간 구성
• 품질 관리 및 공정 개선

핵심 차이점

1. 목적: 파레토 법칙은 자원 배분과 우선순위 설정을 위한 경험적 법칙인 반면, 중심 극한 정리는 표본 평균의 분포 특성을 설명하는 수학적 정리입니다.
2. 적용 방식: 파레토 법칙은 비즈니스 의사결정과 자원 할당에 주로 사용되고, 중심 극한 정리는 통계적 추론과 가설 검정에 사용됩니다.
3. 수학적 엄밀성: 중심 극한 정리는 엄격한 수학적 증명을 가진 정리인 반면, 파레토 법칙은 정확히 80:20 비율이 아닐 수 있는 경험적 관찰입니다.
4. 분포 특성: 파레토 법칙은 멱법칙 분포를 따르는 반면, 중심 극한 정리는 정규 분포와 관련됩니다.

두 개념 모두 통계학에서 중요한 역할을 하지만, 파레토 법칙은 자원 배분과 효율성 향상을 위한 실용적 원칙인 반면 중심 극한 정리는 통계적 추론의 이론적 기반을 제공합니다.

---

1) 기술 통계

1. 평균(Mean) 이상치(이상치의 기준을 적어줘야된다)가 적을때 사용, 평균의함정

• 평균은 전체 데이터를 모두 고려하여 간단하게 산출할 수 있는 대표값으로, 이상치가 적은 경우에 유용하게 사용
• 평균은 극단적인 값(이상치)에 민감하므로, 이상치의 판단 기준을 명확히 해야 합니다. 예를 들어,
    – Z-점수가 ±3 이상인 경우
    – 사분위 범위(IQR)를 이용하여 Q1 – 1.5×IQR 또는 Q3 + 1.5×IQR을 벗어나는 값 등.
• 이상치가 포함되어 있으면 평균 값이 실제 데이터의 중심을 왜곡할 수 있으므로 “평균의 함정”으로 지칭되기도 합니다

2. 중앙값(Median) 내림차순으로 해서 중앙값 시각화하여 확인많이 한다.

• 중앙값은 데이터를 순서대로 정렬한 후 가운데 위치한 값으로, 이상치의 영향을 덜 받습니다.
• 실무에서는 내림차순(또는 오름차순)으로 데이터를 정렬한 후 중앙값을 시각화(예: 박스 플롯)하여 데이터 분포와 극단적인 값의 영향을 확인하는 경우가 많습니다.
• 데이터가 비대칭이거나 이상치가 포함된 경우 중앙값이 보다 현실적인 중심 경향을 제시합니다.

3. 최빈값(Mode) 이상치가 많을땐 (중앙값이나 최빈값을 많이 쓴다)

• 최빈값은 데이터셋 내에서 가장 자주 등장하는 값으로, 특히 이상치가 많거나 범주형 데이터의 경우 유용하게 활용됩니다.
• 수치형 데이터의 경우 값들이 연속적이고 중복이 드물다면 최빈값이 나타나지 않을 수도 있지만, 이상치가 많을 때는 중앙값이나 최빈값이 데이터의 “typical” 상태를 나타내기 위한 보완 도구로 사용됩니다.

4. 최대/최소값(min)

• 최대값과 최소값은 각각 데이터셋에서 가장 큰 수와 가장 작은 수를 나타내며, 데이터의 범위와 분포를 이해하는 데 기여합니다.
• 이 두 값은 이상치일 가능성이 크기 때문에, 이상치를 식별하고 제거하거나 별도로 고려할 때 참고 지표로 활용할 수 있습니다.

5. 이상치(Outlier)

• 이상치는 다른 대부분의 관측값과 크게 벗어난 값으로, 평균 등의 통계치에 큰 영향을 미칠 수 있습니다.
• 이상치 판별 기준은 위에서 언급한 Z-점수, IQR 방법 등 다양한 방법을 사용할 수 있으며, 분석 목적에 따라 이상치 처리가 필요할 수 있습니다.
• 이상치가 적을 경우 평균을 사용할 수 있으나, 이상치가 다수 존재하면 중앙값이나 최빈값 같은 강건한(robust) 척도를 사용하는 것이 일반적

이상치가 적은 경우에는 평균을 사용하여 전체 데이터의 경향성을 파악할 수 있으나, 평균은 극단값에 민감하므로 이상치 기준을 명확히 해야 합니다. 반면, 이상치의 영향을 줄이기 위해 내림차순 정렬 후 시각화하는 중앙값과, 이상치가 많을 때 자주 나타나는 최빈값을 함께 고려하며, 최대/최소값은 데이터의 범위와 이상치 여부를 판단하는 보조 지표로 활용합니다.이와 같이 각각의 척도는 데이터의 특성과 이상치의 존재 여부에 따라 적절한 선택과 활용이 필요

2) 왜도와 첨도 (로그변환을 하여 많이 분석한다)

이 두 지표는 데이터 분포의 모양을 정량적으로 이해하고 이상치를 파악하며, 분석 모델의 적합성을 평가하는 데 매우 유용

왜도 (Skewness)

• 평균, 중앙값, 최빈값은 모두 데이터 집합의 중심을 측정하는 것입니다. 데이터의 왜도는 이러한 양이 서로 어떻게 관련되어 있는지에 따라 결정될 수 있습니다.
• 데이터의 형태를 연구함으로써 평균, 중앙값, 최빈값 간의 관계를 발견할 수 있습니다.
• 피어슨의 첫 번째 방법은 모드를 사용하며 공식은 다음과 같습니다.

  

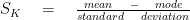
• 두 번째 왜도 공식은 중앙값을 사용하며 다음과 같이 표시됩니다.

  

• Bowley의 사분위수별 왜도 측정 방법은 다음과 같습니다.

  

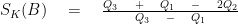
기억하자면, 우리는 이전 장의 '평균'에서 평균, 중앙값, 최빈값에 대해 공부했고, 다양한 공식을 사용하여 이를 찾는 방법을 배웠습니다. 우리는 일반적으로 이것들이 주어진 세트에 대해 동일한 수치 값을 제공하지 않는다고 말했습니다. 그러나 만약 우리가 세 가지 모두 동일한 수치 값을 제공한다는 것을 발견한다면 그 데이터는 대칭적 데이터로 알려져 있습니다. 따라서 이것은 데이터 세트가 대칭인지 아닌지를 검증하는 좋은 방법이라고 할 수 있습니다.

비대칭 데이터라고 알려진 다른 유형의 데이터 세트가 있습니다. 비대칭 분포는 왜도가 대칭에서 벗어남을 측정하는 왜곡된 분포입니다.

평균 > 중앙값인 경우 분포가 양의 비대칭임을 나타냅니다.
평균 < 중앙값인 경우 분포가 음의 비대칭임을 나타냅니다.

출처 : https://alevelmaths.co.uk/statistics/skewness/

우리는 또한 칼 피어슨의 왜도 측정을 사용하여 데이터의 왜도를 측정할 수 있습니다. 그는 표본의 왜도를 찾는 두 가지 방법을 개발했습니다.

첫 번째 방법은 모드와 그 공식을 사용합니다.

그러나 이 방법은 모드가 너무 적은 조각으로 구성된 데이터의 경우 그다지 안정적이지 않은 것으로 간주됩니다. 왜냐하면 중심 경향을 측정하는 데 그다지 강력한 방법으로 간주되지 않기 때문입니다.

예를 들어 첫 번째 데이터 세트에서 8 미만은 두 번만 발생하므로 피어슨의 첫 번째 왜도 공식을 사용할 때는 중심 경향을 측정하는 데 적합하지 않으므로 주의해야 합니다. 그러나 두 번째 세트에서는 8이 10번 나타나는 것을 볼 수 있으므로 피어슨의 왜도 측정을 사용하면 더 안정적이고 신뢰할 수 있는 결과를 얻을 수 있습니다.

세트 1 = [1, 2, 3, 4, 5, 8, 7, 8]

세트 2 = [1, 5, 6, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8]

게다가 피어슨의 두 번째 왜도 공식은 중앙값을 사용하며 다음과 같이 표시됩니다.

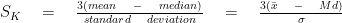
칼 피어슨의 왜도계수는 -3과 +3 사이입니다.

SK = 0이면 빈도 분포가 정규적이고 대칭적이라고 할 수 있습니다.
SK < 0이면 빈도 분포가 음으로 비대칭적이라고 할 수 있습니다.
SK > 0이면 빈도 분포가 양으로 비대칭적이라고 할 수 있습니다.

• 정의
  왜도는 데이터 분포의 좌우 비대칭성을 나타내는 척도로, 데이터 값들이 평균을 중심으로 얼마나 치우쳐 있는지를 수치로 표현합니다.
• 해석
  ─ 왜도 값이 0이면 분포가 좌우 대칭임을 의미합니다.
  ─ 양의 왜도는 오른쪽 꼬리가 길어 오른쪽으로 치우친 분포를, 음의 왜도는 왼쪽 꼬리가 길어 왼쪽으로 치우친 분포를 나타냅니다.
  ─ 일반적으로 |왜도| < 0.5이면 분포가 상당히 대칭적, 0.5 ~ 2이면 적당히 치우쳐 있으며, 2보다 크면 큰 비대칭성을 가진다고 판단합니다.
• 계산 방법
  주로 3차 중심모멘트를 기준으로 계산하며, 피어슨의 비대칭 계수를 이용하여 평균, 중앙값, 최빈값 간의 관계로도 해석할 수 있습니다.

첨도 (Kurtosis)

• 정의
  첨도는 데이터 분포의 뾰족함(peakness)과 꼬리의 두꺼움을 나타내는 척도입니다. 즉, 분포의 중심부에 데이터가 얼마나 집중되어 있고 꼬리 부분이 두꺼운지를 수치로 표현합니다.
• 해석
  ─ 정규분포의 첨도는 보통 3으로 정의되며, 이를 기준으로 판단합니다.
  ─ 3보다 큰 경우(혹은 Excess Kurtosis가 0보다 큰 경우)는 분포가 정규분포보다 중심이 뾰족하고 꼬리가 두꺼워 이상치가 많을 가능성이 있음을 의미하며(Leptokurtic),
  ─ 3보다 작은 경우(혹은 Excess Kurtosis가 음수)는 분포가 평탄하고 꼬리가 얇음을 나타냅니다(Platykurtic).
• 계산 방법
  4차 중심모멘트를 표준편차의 4제곱으로 나누어 계산하며, Fisher’s 정의에서는 정규분포의 첨도가 0이 되도록 3을 빼서 Excess Kurtosis로 표현하기도 합니다
  
  

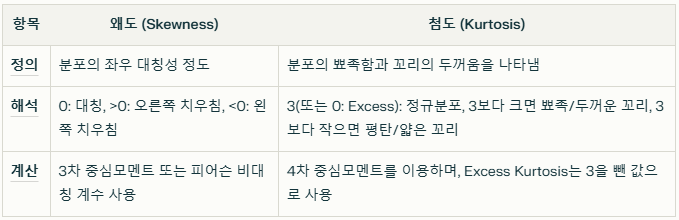
데이터 분포의 모양을 설명할 때, 우리는 또한 꼬리가 얼마나 극단적인지를 특성화하여 이상치 또는 극단적인 관찰치에 대한 잠재적 문제를 식별하는 데 도움이 될 수 있습니다. 첨도는 분포의 중심과 꼬리 사이에 데이터가 어떻게 분산되는지 측정하는 데 사용되는 설명 적 통계 로, 값이 클수록 데이터 분포에 관찰치가 두껍게 집중되어 있거나 극단적인 관찰치가 긴 "무거운" 꼬리가 있을 수 있음을 나타냅니다. 분포의 첨도는 다음을 포함한 다양한 공식을 사용하여 계산할 수 있습니다.

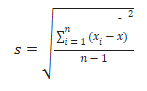
각 값이 평균에서 떨어진 표준화된 거리가 4제곱되기 때문에 평균과 다르지만 평균 위 또는 아래에 표준편차 1개 이상 있고 데이터 분포의 꼬리에 있는 관측치 의 영향을 가장 많이 받는 모든 관측치에 대해 첨도가 증가합니다.예를 들어, 그림 5 의 왼쪽에 있는 데이터 분포와 유사한 단봉형 종 모양 분포인 정규 분포는 첨도가 3이고, 분포의 대부분이 평균 주위에 집중되어 있고 꼬리의 높이는 빠르게 0에 접근합니다.정규 분포는 종종 다른 분포를 비교하기 위한 기준 분포 역할을 하기 때문에 분포의 첨도 값은 일반적으로 해당 분포의 첨도와 정규 분포의 첨도의 차이 또는 "초과 첨도"로 보고됩니다. 중간고사 점수의 2학년 분포( 그림 4 )와 같이 과잉 첨도의 양수 값을 갖는 데이터 분포는 정규 분포보다 꼬리가 두꺼운 경향이 있는 반면, 그림 5 에 표시된 대략 균일한 데이터 분포와 같이 과잉 첨도의 음수 값을 갖는 분포 는 극단적인 관측치가 거의 없거나 전혀 없는 더 광범위한 분포가 되는 경향이 있습니다. 일반적으로 과잉 첨도의 양수 값이 높을수록 데이터에 이상치 문제가 있을 수 있음을 시사하며, 이는 데이터의 정확도를 확인하고 그래픽으로 요약하여 추가로 탐색해야 할 데이터 분포에 대한 추가 정보를 제공합니다. 
첨도는 분포의 꼬리가 정규 분포 의 꼬리와 얼마나 다른지를 설명하는 척도입니다 . 표본 첨도는 다음 방정식을 사용하여 계산할 수 있습니다.

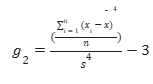
첨도 값이 양수이면 두꺼운 꼬리가 있음을 시사합니다. 반대로 음수 값은 가벼운 꼬리가 있음을 의미합니다. 꼬리의 무거움이나 가벼움은 정규 분포와 비교되며 데이터 분포가 정규 분포보다 평평하거나 덜 평평한지 여부를 시사합니다. 표준 정규 분포 의 경우 첨도 값은 3.0입니다 . 첨도는 그림  에서와 같이 세 가지 측정으로 분류할 수 있습니다 . 분포의 첨도 통계량 이 정규 분포 또는 종 모양 곡선 과 유사 하면 중형 분포라고 합니다. 이러한 유형의 분포는 정규 분포와 유사한 극단 값 특성을 갖습니다 . 첨도가 중형 분포보다 크면 렙토쿠르틱 분포라고 합니다. 이 분포는 긴 꼬리를 갖습니다(많은 이상치가 있기 때문). 이상치는 수평 축을 늘리고 많은 데이터가 좁은 곡선에 나타납니다. 마지막 유형의 분포는 플라티쿠르틱 분포이며 중형 분포보다 첨도가 작습니다. 이 유형의 분포는 짧은 꼬리를 갖습니다(이상치가 적기 때문). 정규 분포와 비교할 때 이러한 분포는 극단값이 적습니다.

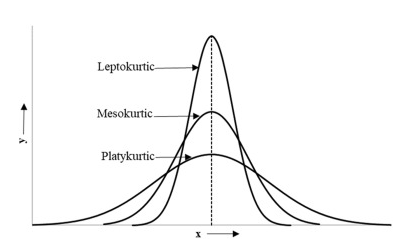
왜도와 첨도를 정의하려면 먼저 분포의 발생을 고려해야 합니다. 분포는 변수의 모든 가능한 값과 각 값의 발생 빈도를 보여줍니다. 이는 표나 함수를 사용하여 가장 자주 표시됩니다. 발생 빈도를 시각화하는 또 다른 방법은 히스토그램입니다. 히스토그램은 구성하기가 다소 간단하지만 분포의 모양을 결정하는 가장 좋은 방법은 아닙니다. 히스토그램의 모양은 선택하는 빈의 수에 크게 영향을 받기 때문입니다. 예를 들어, 빈 너비는 히스토그램이 발생률이 높은 국소 영역을 식별하는 능력에 영향을 미칩니다. 빈이 너무 크면 충분한 차별화를 얻을 수 없습니다. 빈이 너무 작으면 데이터를 그룹화할 수 없습니다. 따라서 분포 커널 밀도 플롯의 모양을 결정하는 것이 더 적절한 방법입니다.

변수의 분포를 고려할 때, 왜도는 분포의 비대칭 정도를 측정하는 것으로 간주됩니다. 분포의 작은 끝(왼쪽 꼬리)에 있는 꼬리가 분포의 큰 끝(오른쪽 꼬리)에 있는 꼬리보다 더 두드러지면 함수는 음의 왜도를 갖는다고 합니다. 그 반대인 경우 양의 왜도를 갖는다고 합니다. 두 꼬리가 같으면 왜도가 0입니다. 왜도와 마찬가지로 첨도는 분포의 모양을 설명하지만 분포에서 이상치가 존재하는 정도를 나타냅니다. 분포의 네 번째 중심 모멘트 의 정규화된 형태로 정의됩니다.

 

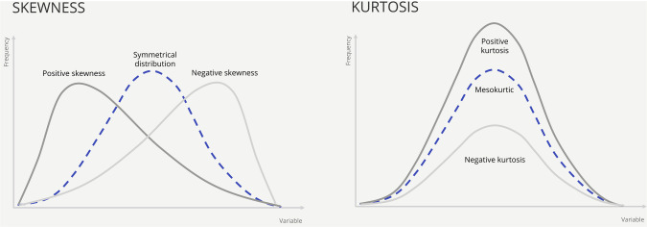
데이터 분석에서의 활용

• 정규성 검증
  회귀분석과 같은 모수적 통계 분석에서는 잔차의 정규성을 전제로 하므로 왜도와 첨도를 활용하여 데이터가 정규분포에 가까운지를 확인합니다.
• 이상치 탐지
  첨도는 특히 이상치(outlier)의 존재 여부를 파악하는 데 도움이 됩니다. 높은 첨도는 꼬리가 두꺼워 극단치가 많음을 시사하므로 데이터 정제 과정에서 주의해야 합니다.
• 분포 특성 파악
  왜도와 첨도를 함께 분석하면 데이터가 어느 방향으로 치우쳐 있으며 분포가 뾰족한지 평탄한지 쉽게 파악할 수 있어, 적절한 통계 기법이나 전처리 방법을 선택하는 데 유용합니다.

왜도는 데이터의 좌우 비대칭성을, 첨도는 분포의 뾰족함과 꼬리의 특성을 나타내며, 이 두 지표를 통해 데이터의 분포 형태를 다각도로 파악할 수 있습니다. 이러한 분석은 데이터 전처리 및 모델링에 중요한 정보를 제공합니다.

 

RFM이 중요하다

확률과 통계관련 추천책 :
ISLR(현업에서 공부), 오랄리에 데이터과학을 위한 통계, 가장쉬운 통계학, A/B 테스트, 실리콘벨리의 실험실
세상에서 가장쉬운 통계학입문, 빅데이터를 지탱하는 기술(테이터 웨이하우스와 비교해서 추천),
대시보드 설계와 데이터 시각화, 데이터 분석가의 숫자유감, 실무로 통하는 인과추론 with파이썬, 월스트리트저널 인포그래픽 가이드, 루커스튜디오, 데이터 분석을 위한 SQL 레시피(어렵지만 실무와 가장가깝다), solvesql
프로젝트 성패를 결정짓는 데이터 모델링 이야기, 데이터 중심 애플리케이션 설계(상)

데이터로 가치를 만드는 Steven, Follow on LinkedIn