320x100
728x90
ADsP시험 내용 중 용어 중심으로 정리 하였습니다.
Accuracy와 Precision
1) Accuracy (정확도) : "전체 중에서 맞춘 것", "중앙을 맞췄는가?"
- 전체 데이터 중에서 정답을 맞춘 비율을 의미함.
- 공식:
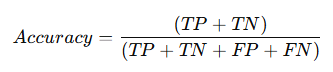
- TP (True Positive) ↑ : 실제 긍정(Positive)이고 예측도 Positive(긍정), Accuracy가 높으므로 TP가 많은 편
- TN (True Negative) ↑ : 실제 Negative(부정)이고, 예측도 Negative(부정), Accuracy가 높으므로 TN도 많은 편
- FP (False Positive) ↑ : 실제 Negative(부정)인데, 예측을 Positive(긍정),
Precision이 낮다는 것은 긍정으로 예측한 것 중에서 틀린 비율(FP)이 높다는 것.
모델이 긍정이라고 예측한 것 중 실제 부정(FP)이 많음 - FN (False Negative) ↓ : Accuracy가 높기 때문에 FN이 많지는 않음,
실제 Positive(긍정)인데 Negative(부정)로 잘못 예측하는 경우가 적음
2) Precision (정밀도) : "맞다고 한 것 중에서 진짜 맞은 비율", "화살이 한 곳에 모여 있는가?"
- 모델이 긍정(Positive)이라고 예측한 것들 중에서 실제로 긍정인 비율을 의미함.
- 공식:
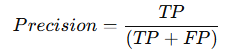
- 즉, False Positive(거짓 긍정)를 얼마나 줄이느냐가 핵심
- 의료 진단, 스팸 필터링 등에서 중요하게 사용됨.
(예: 암 진단에서 양성으로 예측한 경우가 실제 암 환자인지 확인하는 것이 중요)
Accuracy 높음, Precision 높음 → TP↑, TN↑, FP↓ , FN↓
예측이 매우 정확하여 긍정(Positive)과 부정(Negative) 모두 잘 맞춤
- FP↓: 건강한 사람을 암이라고 잘못 진단하는 경우 거의 없음
- FN↓: 암 환자를 건강하다고 놓치는 경우 거의 없음
Accuracy 높음, Precision 낮음 → TP↑, TN↑, FP↑, FN↓
전체적으로 맞춘 개수(TP+TN)는 많지만, Precision이 낮음 (FP가 많음)
- FP↑: 건강한 사람도 암이라고 잘못 예측하는 경우 많음 (Precision 낮음 원인!)
- FN↓: 암 환자를 놓치는 경우는 적음
Accuracy 낮음, Precision 높음 → TP↓, TN↓, FP↓, FN↑
긍정이라고 예측한 것(TP+FP) 중에서 실제 맞는 비율(Precision)은 높음 (FP 적음), 하지만 전체 Accuracy는 낮음 → (FN 많음, TN 적음)
- FP↓: 건강한 사람을 암이라고 잘못 예측하는 경우 거의 없음 (Precision이 높은 이유!)
- FN↑: 암 환자를 건강하다고 놓치는 경우 많음 (Accuracy가 낮아지는 이유!)
Accuracy 낮음, Precision 낮음 → TP↓, TN↓, FP↑, FN↑
예측이 엉망이라 맞춘 개수(TP+TN)도 적고, Precision(정밀도)도 낮음, 즉, FP도 많고 FN도 많음 → Accuracy와 Precision 둘 다 낮음
- FP↑: 건강한 사람을 암이라고 잘못 예측하는 경우 많음
- FN↑: 암 환자를 건강하다고 놓치는 경우 많음

- Accuracy 높음, Precision 높음 🔵 → 모델이 정확하고 신뢰할 수 있음
- Accuracy 높음, Precision 낮음 🟡 → 정답을 많이 맞추지만, 긍정 예측의 신뢰도가 낮음 (FP 많음)
- Accuracy 낮음, Precision 높음 🔴 → 긍정을 조심스럽게 예측해서 Precision은 높지만, 전체 Accuracy가 낮음 (FN 많음)
- Accuracy 낮음, Precision 낮음 ⚫ → 엉망인 모델 (FP, FN 둘 다 많음)
'데이터 분석가:Applied Data Analytics > ADsP' 카테고리의 다른 글
| 회귀분석에서 연속형 종속변수를 예측하는 방법 (0) | 2025.02.22 |
|---|---|
| 회귀분석은 종속변수가 연속형일때 사용 (0) | 2025.02.22 |
| 확률과 통계 (0) | 2025.02.20 |
| ADsP 예상문제 내용 (0) | 2025.02.14 |
| ADsP의 예상 기출문제 (0) | 2025.02.14 |