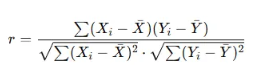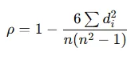EDA를 효과적으로 훈련하기 위한 단계
1. 데이터 이해 및 준비
•데이터의 구조 파악: `head()`, `tail()`, `info()`, `describe()` 등을 사용해 데이터의 기본 정보를 확인합니다.
•결측치 및 이상치 확인: 결측값(`isnull()`), 이상치(박스플롯 등)를 찾아내고 처리합니다.
•데이터 타입 확인 및 변환: 각 열의 데이터 유형을 확인하고 필요 시 변환합니다.
2. 기초 통계 분석
•평균, 중앙값, 표준편차 등 주요 통계값을 계산하여 데이터 분포를 이해합니다.
•속성 간 상관관계 분석: `corr()` 함수와 히트맵(Heatmap)을 사용해 변수 간 관계를 시각화합니다.
3. 시각화를 통한 탐색
•히스토그램, 박스플롯, 산점도 등을 활용해 데이터를 다양한 각도에서 시각화합니다.
•Seaborn, Matplotlib, Plotly 등의 라이브러리를 사용하여 데이터를 직관적으로 표현합니다.
4. 패턴 및 가설 발견
•데이터를 탐색하며 흥미로운 패턴을 발견하고 이를 바탕으로 가설을 세웁니다.
•반복적인 탐색 과정을 통해 가설을 수정하거나 새로운 질문을 도출합니다.
회귀모형의 가정
- 선형성(Linearity): 독립변수와 종속변수 간 관계가 선형이어야 함
- 정규성(Normality): 오차항(residual)이 정규분포를 따라야 함
- 등분산성(Homoscedasticity): 오차항의 분산이 일정해야 함
- 독립성(Independence): 각 관측값 간 독립성을 유지해야 함
- 다중공선성(Multicollinearity): 독립변수 간 강한 상관관계를 피해야 함
상관관계(Correlation) 분석 방법
상관관계란 두 변수 간의 관련성을 의미하며, 한 변수가 변할 때 다른 변수가 어떤 경향을 보이는지를 나타냅니다.
(1) 정의
- 두 변수가 서로 어떻게 관련되는지의 강도와 방향을 나타냄
- 원인과 결과 관계는 명확하지 않음(단순 관련성만을 나타냄)
(2) 분석 방법
- 산점도(Scatter Plot)
- 두 변수의 관계를 시각적으로 표현해 직관적으로 파악하는 방법
- 상관계수(Correlation Coefficient)
- 대표적인 계수: 피어슨(Pearson), 스피어만(Spearman), 켄달(Kendall)
- –1 ≤ r ≤ 1, ±1에 가까울수록 상관이 강함
- 0에 가까울수록 상관관계 없음
- 1에 가까움: 강한 양(+)의 상관
- 1에 가까움: 강한 음(-)의 상관
(3) 주의사항
- 상관관계는 인과관계를 나타내지 않으며, 높은 상관이 있다고 해서 원인-결과로 해석하면 안됨
1. 피어슨 상관계수 (Pearson’s rrr)
- 정의: 두 변수 간의 선형 상관관계를 측정하는 지표
- 값 범위: −1≤r≤1
- 수식 :
- 특징:
- 선형 관계(linear relationship)만 측정 가능
- 두 변수가 정규 분포를 따를 때 적절하게 사용됨
- 이상치(outlier)에 민감함
- 해석:
- r=1r = 1r=1: 완벽한 양의 선형 관계
- r=−1r = -1r=−1: 완벽한 음의 선형 관계
- r=0r = 0r=0: 선형 관계 없음 (비선형 관계는 있을 수 있음)
2. 스피어만 상관계수 (Spearman’s ρ\rhoρ)
- 정의: 두 변수 간의 순위(랭크) 기반 상관관계를 측정하는 지표
- 값 범위: −1≤ρ≤1
- 수식:
- 특징:
- 비선형 관계도 측정 가능 (단조 증가/감소 관계)
- 두 변수가 정규성을 따르지 않아도 사용 가능
- 이상치(outlier)에 덜 민감함
- 해석:
- ρ=1: 순위가 완벽히 일치 (완벽한 단조 증가 관계)
- ρ=−1: 순위가 완전히 반대 (완벽한 단조 감소 관계)
- ρ=0: 순위 간 상관관계 없음 (단조 관계 없음)
3. 언제 어떤 상관계수를 사용할까?
| 구분 | 피어슨 상관계수 | 스피어만 상관계수 |
| 데이터 관계 | 선형 관계 | 단조 관계 (비선형도 가능) |
| 데이터 분포 | 정규분포 | 비정규분포 가능 |
| 이상치 영향 | 민감함 | 둔감함 |
| 데이터 유형 | 연속형 변수 | 순위형(서열) 변수 가능 |
- 피어슨 사용 예시:
- 키와 몸무게 간의 관계 (연속형, 선형 관계)
- 매출과 광고비 간의 관계 (정규분포 가정 가능)
- 스피어만 사용 예시:
- 학생의 시험 성적과 순위 (서열 데이터)
- SNS 활동량과 수익 간의 관계 (비선형 가능성 있음)
- 피어슨 상관계수는 선형 관계를 측정하며, 정규성을 가정하고 이상치에 민감함.
- 스피어만 상관계수는 비선형적인 단조 관계도 측정 가능하고, 정규성 가정 없이 사용 가능하며 이상치에 강건함.
- 데이터의 특성(정규성, 이상치 존재 여부, 선형/비선형 관계)을 고려하여 적절한 상관계수를 선택해야 함.
- 대푯값: 자료를 대표하는 값
- 평균(Mean, xˉ\bar{x}): xˉ=∑xin\bar{x} = \frac{\sum x_i}{n}
- 중앙값(Median): 데이터를 크기순으로 정렬했을 때 중앙에 위치한 값
- 최빈값(Mode): 가장 자주 나오는 값
- 산포도: 데이터가 퍼져 있는 정도
- 분산(Variance, s2s^2): s2=∑(xi−xˉ)2ns^2 = \frac{\sum (x_i - \bar{x})^2}{n}
- 표준편차(Standard Deviation, ss): s=s2s = \sqrt{s^2}
- 이항분포(Binomial Distribution): 성공 확률이 pp인 시행을 nn번 했을 때의 확률
- 확률 함수: P(X=k)=C(n,k)pk(1−p)n−kP(X = k) = C(n, k) p^k (1-p)^{n-k}
- 정규분포(Normal Distribution): 데이터가 종 모양으로 분포하는 경우
- 평균 μ\mu, 표준편차 σ\sigma를 갖는 정규분포: N(μ,σ2)N(\mu, \sigma^2)
- 표준정규분포: N(0,1)N(0, 1)
통계적 시각화 기법들은 데이터의 분포와 관계를 직관적으로 이해하는 데 중요한 역할을 합니다. 주요 시각화 기법들
1. 도수분포표 (Frequency Table)
개념
- 연속형 데이터를 일정한 구간(bin)으로 나누고, 각 구간에 속하는 데이터 개수를 정리한 표
- 데이터의 분포를 요약하여 이해하는 데 도움을 줌
주요 개념
- 계급(class interval): 데이터를 일정한 구간으로 나눈 것
- 도수(frequency): 각 계급에 속하는 데이터의 개수
- 상대도수(relative frequency): 전체 데이터에서 해당 계급이 차지하는 비율
- 누적도수(cumulative frequency): 해당 계급까지의 총 도수
활용
- 데이터를 요약하여 히스토그램 등의 시각화 자료로 활용
2. 히스토그램 (Histogram)
- 도수분포표를 막대그래프로 시각화한 형태
- 연속형 데이터의 분포를 한눈에 파악할 수 있음
특징
- 가로축: 계급(구간)
- 세로축: 도수(빈도)
- 막대 간격이 없고, 연속적으로 이어져 있음 (막대그래프와 차이점)
활용
- 데이터가 어떻게 분포하는지 확인 (정규분포 여부, 이상치 탐색 등)
- 도수분포표를 직관적으로 표현할 때 사용
3. 막대그래프 (Bar Chart)
- 범주형(이산형) 데이터의 빈도를 비교하는 그래프
- 각 범주의 빈도를 막대의 길이로 표현
특징
- 막대 간격이 존재 (히스토그램과 차이점)
- 세로형(Vertical)과 가로형(Horizontal) 형태로 표현 가능
활용
- 범주형 데이터의 개수를 비교할 때 사용
- 예: 과목별 학생 수, 제품별 판매량 비교
4. 파이차트 (Pie Chart)
- 전체 데이터에서 각 범주가 차지하는 비율을 원형으로 표현하는 그래프
특징
- 각 조각의 크기는 백분율(%)로 나타냄
- 전체의 합이 100%를 초과하면 안 됨
활용
- 전체 대비 개별 항목의 비율을 비교할 때 사용
- 예: 시장 점유율, 인구 분포
단점
- 범주가 많을 경우 해석이 어려움
- 데이터 간의 차이를 직관적으로 비교하기 어려움 (막대그래프가 더 적절할 수 있음)
5. 산점도 (Scatter Plot)
- 두 개의 연속형 변수 간의 관계를 점으로 표현한 그래프
특징
- 가로축(X): 독립변수
- 세로축(Y): 종속변수
- 상관관계 분석 가능
- 양의 상관관계: X 증가 → Y 증가
- 음의 상관관계: X 증가 → Y 감소
- 무상관: X, Y 간 관계 없음
활용
- 변수 간 관계 분석 (예: 키와 몸무게, 공부 시간과 성적)
- 이상치(outlier) 탐색
6. 줄기-잎 그림 (Stem-and-Leaf Plot)
- 데이터를 줄기(stem)와 잎(leaf)으로 나누어 정리하는 방식
- 도수분포표와 히스토그램을 대체할 수 있음
특징
- 줄기(stem): 데이터의 십의 자리 (또는 백의 자리)
- 잎(leaf): 데이터의 일의 자리
- 히스토그램과 유사하지만 원본 데이터를 유지한다는 장점이 있음
활용
- 데이터의 분포를 한눈에 확인할 때 사용
- 작은 데이터셋의 분포를 쉽게 파악 가능
7. 상자수염그림 (Box Plot)
- 데이터의 분포와 이상치를 시각적으로 표현하는 그래프
- 다섯 가지 요약값을 사용하여 데이터의 변동 범위를 나타냄
다섯 가지 요약값
- 최솟값 (Min): 가장 작은 값
- 제1사분위수 (Q1, 25%): 하위 25%에 해당하는 값
- 중앙값 (Median, Q2, 50%): 데이터의 중앙값
- 제3사분위수 (Q3, 75%): 상위 25%를 제외한 값
- 최댓값 (Max): 가장 큰 값
이상치(Outlier) 탐지 방법
- 이상치 기준:
- Q1 - 1.5 × IQR 미만
- Q3 + 1.5 × IQR 초과
- IQR(Interquartile Range) = Q3 - Q1
활용
- 데이터의 변동 범위를 쉽게 파악
- 이상치를 탐지하여 데이터 정제에 활용
정리: 빅데이터분석기사 필기에서 중요한 차이점시각화 기법 데이터 유형 특징 활용
| 시각화 기법 | 데이터 유형 | 특징 | 활용 |
| 도수분포표 | 연속형 | 데이터를 구간별로 나누어 빈도를 정리 | 히스토그램 작성 시 사용 |
| 히스토그램 | 연속형 | 막대가 붙어 있음 | 데이터의 분포 확인 |
| 막대그래프 | 범주형 | 막대 간격이 있음 | 카테고리별 비교 |
| 파이차트 | 범주형 | 비율(%) 표현 | 전체 대비 구성 요소 비교 |
| 산점도 | 연속형 | 두 변수 관계 분석 | 상관관계 탐색 |
| 줄기-잎 그림 | 연속형 | 데이터 원본 유지 | 작은 데이터셋의 분포 확인 |
| 상자수염그림 | 연속형 | 사분위수와 이상치 표현 | 데이터 분포와 이상치 탐색 |
빅데이터분석기사 필기 대비 팁
- 히스토그램 vs. 막대그래프 구분
- 히스토그램: 연속형 데이터, 막대가 붙어 있음
- 막대그래프: 범주형 데이터, 막대 간격이 있음
- 상자수염그림의 다섯 가지 요약값 숙지
- 이상치 판별 기준(Q1 - 1.5×IQR, Q3 + 1.5×IQR)
- 도수분포표 → 히스토그램 변환 가능
- 도수분포표를 작성하면 히스토그램을 쉽게 생성 가능
- 산점도에서 상관관계 읽기
- 점이 대각선 방향으로 정렬되면 상관관계 존재
'데이터 분석가:Applied Data Analytics > 자격증(ADsP,빅분기 등)' 카테고리의 다른 글
| 빅분기필기-고급 분석기법 (0) | 2025.03.25 |
|---|---|
| 추론통계 (0) | 2025.03.17 |
| 빅분기 스터디 내용1 (0) | 2025.03.17 |
| 빅분기 계산문제 (0) | 2025.03.15 |
| 주말 빅분기 공부 계획 (1) | 2025.03.09 |