데이터 분석가:Applied Data Analytics/판다스 데이터분석

머신러닝(Machine Learning, ML)-용어편

데이터분석 2025. 2. 14. 10:18

320x100

머신러닝과 관련된 개념과 분석방법들에 대해 미리 용어들의 내용을 정리 했습니다.

정리하다 보니 너무 내용이 이해가 안되서 다시 아래 □안에 핵심정리로 따로 정리 해보았습니다.

1. 머신러닝 전체 프로세스

머신러닝 프로젝트는 보통 다음과 같은 과정으로 진행된다.

문제 정의 및 목표 설정
데이터 수집 및 전처리
데이터 탐색 및 분석
모델 선택 및 학습
모델 평가 및 성능 개선
모델 배포 및 활용

이제 각 단계를 구체적으로 설명하고, 사용되는 분석 방법을 소개하겠다.

2. 머신러닝 프로세스 상세 설명 & 분석 방법

1) 문제 정의 및 목표 설정

머신러닝을 적용할 문제를 정의하고, 목표를 설정하는 단계이다.

예제:
- 이메일이 스팸인지 아닌지 분류
- 고객이 제품을 구매할지 예측
- 집의 크기와 위치를 보고 집값을 예측

머신러닝 유형 선택
문제 유형에 따라 머신러닝의 학습 방식이 달라진다.

지도 학습 (Supervised Learning) → 정답(Label)이 있는 경우
- 예제: 스팸 메일 분류, 집값 예측
비지도 학습 (Unsupervised Learning) → 정답(Label)이 없는 경우
- 예제: 고객 세분화, 이상 탐지
강화 학습 (Reinforcement Learning) → 보상을 통해 최적의 행동 학습
- 예제: 알파고, 자율주행

2) 데이터 수집 및 전처리

머신러닝 모델을 만들려면 좋은 데이터가 필요하다.

데이터가 충분히 많을수록 모델 성능이 좋아진다.
데이터에 이상치나 결측치가 있다면, 적절히 처리해야 한다.

사용되는 분석 방법

결측치 처리 (누락된 데이터 보정)
- df.fillna(평균값) → 평균값으로 결측치 대체
- df.dropna() → 결측값이 있는 행 삭제
이상치 탐색 (극단적인 값 제거)
- 박스플롯 (Boxplot) 분석 → 이상치 시각화
- Z-score 분석 → 특정 기준(Z 값)을 넘는 값 제거
데이터 스케일링 (정규화, 표준화)
- MinMaxScaler → 모든 값을 0~1 범위로 조정
- StandardScaler → 평균 0, 표준편차 1로 변환
  
  from sklearn.preprocessing import MinMaxScaler, StandardScaler
  
  scaler = MinMaxScaler() # 0~1 범위로 정규화
  
  X_scaled = scaler.fit_transform(X)

3) 데이터 탐색 및 분석

모델 학습 전에 데이터의 특징을 분석하는 단계이다.
사용되는 분석 방법

기초 통계 분석 (describe())
- 평균, 최댓값, 최솟값, 분산 확인
시각화 분석 (matplotlib, seaborn)
- sns.pairplot(df) → 변수 간 관계 분석
- sns.heatmap(df.corr()) → 변수 간 상관관계 분석
상관계수 분석 (어떤 변수가 종속 변수에 영향을 미치는지 확인)
- df.corr() → 변수 간 관계를 수치화
  
  import seaborn as sns
  
  import matplotlib.pyplot as plt
  
  # 상관계수 히트맵
  
  plt.figure(figsize=(8, 6))
  
  sns.heatmap(df.corr(), annot=True, cmap="coolwarm")
  
  plt.show()

4) 모델 선택 및 학습

문제 유형에 따라 적절한 머신러닝 알고리즘을 선택하고 학습한다.
사용되는 머신러닝 알고리즘

회귀 분석 (Regression)
- 단순 선형 회귀: Y = aX + b (직선 관계)
- 다중 회귀: 여러 개의 독립 변수를 활용
- 다항 회귀: Y = aX² + bX + c (곡선 관계)
  
  from sklearn.linear_model import LinearRegression
  
  model = LinearRegression() # 선형 회귀 모델 생성
  
  model.fit(X_train, Y_train) # 모델 학습

분류 모델 (Classification)
- 로지스틱 회귀 → 0 or 1 예측 (예: 스팸 메일 분류)
- KNN (K-최근접 이웃) → 가까운 이웃을 기준으로 예측
- SVM (서포트 벡터 머신) → 초평면을 이용한 분류
- 의사결정나무 (Decision Tree) → 트리 구조 기반 예측
  
  from sklearn.tree import DecisionTreeClassifier
  
  model = DecisionTreeClassifier(max_depth=3) # 의사결정나무 모델 생성
  
  model.fit(X_train, y_train) # 모델 학습

비지도 학습 (Unsupervised Learning)
- K-Means 군집화 → 비슷한 데이터끼리 그룹화
- DBSCAN → 이상값 탐지, 밀도 기반 군집화
  
  from sklearn.cluster import KMeans
  
  kmeans = KMeans(n_clusters=3) # 3개의 그룹으로 군집화
  
  kmeans.fit(X)

5) 모델 평가 및 성능 개선

모델이 학습된 후, 테스트 데이터를 활용하여 성능을 평가한다.
사용되는 평가 방법

회귀 모델 평가 지표
- MSE (Mean Squared Error, 평균 제곱 오차)
- R² Score (결정 계수, 설명력 측정)
  
  from sklearn.metrics import mean_squared_error, r2_score
  
  mse = mean_squared_error(Y_test, Y_pred)
  
  r2 = r2_score(Y_test, Y_pred)

분류 모델 평가 지표
- 정확도 (Accuracy Score)
- 정밀도 (Precision) & 재현율 (Recall)
  
  from sklearn.metrics import accuracy_score
  
  accuracy = accuracy_score(y_test, y_pred)

과대적합(Overfitting) 방지 방법

정규화 (Regularization) 적용
교차 검증 (Cross Validation) 활용
훈련 데이터와 검증 데이터 분리
조기 종료(Early Stopping) 적용

from sklearn.model_selection import cross_val_score

scores = cross_val_score(model, X, y, cv=5) # 5-fold 교차 검증

print(f"평균 정확도: {scores.mean():.4f}")

6) 모델 배포 및 활용

학습된 모델을 실제 환경에서 활용하는 단계이다.

API로 배포: Flask, FastAPI를 활용하여 서버에 배포
웹 앱으로 연동: 웹 사이트나 모바일 앱에서 사용
실시간 예측 시스템 구축

3. 정 리

문제 정의 및 목표 설정 → 어떤 문제를 해결할 것인지 결정
데이터 수집 및 전처리 → 결측치, 이상치 처리, 정규화
데이터 탐색 및 분석 → 데이터 시각화, 상관관계 분석
모델 선택 및 학습 → 회귀, 분류, 군집화 알고리즘 활용
모델 평가 및 성능 개선 → MSE, R² Score, Accuracy 활용
모델 배포 및 활용 → API, 웹 서비스, 실시간 예측 적용

머신러닝(Machine Learning, ML)은 데이터를 기반으로 컴퓨터가 스스로 패턴을 학습하고, 이를 활용해 미래를 예측하거나 의사 결정을 자동화하는 기술이다.
즉, 사람이 일일이 규칙을 프로그래밍하지 않아도, 데이터를 통해 알아서 규칙을 발견하고 새로운 데이터에 적용하는 것이다.

1. 머신러닝의 핵심 개념

머신러닝은 다음과 같은 핵심 개념을 기반으로 작동한다.

(1) 데이터

머신러닝의 학습은 데이터에서 시작된다.
데이터는 숫자, 텍스트, 이미지 등 다양한 형태로 존재할 수 있다.
좋은 데이터를 많이 확보할수록 좋은 성능을 기대할 수 있다.

(2) 패턴 학습 (모델 학습)

컴퓨터는 주어진 데이터를 분석하여 패턴을 찾아내는 모델(model)을 만든다.
이 모델은 새로운 데이터가 주어졌을 때 예측을 수행할 수 있다.

(3) 평가 및 개선

학습된 모델이 얼마나 정확한지 평가하고, 잘못된 점을 수정하여 성능을 향상시킨다.

2. 머신러닝의 주요 유형

머신러닝은 크게 지도 학습, 비지도 학습, 강화 학습 세 가지로 나뉜다.

(1) 지도 학습 (Supervised Learning)

입력 데이터(특성, X)와 정답(레이블, Y)이 주어진 상태에서 학습하는 방식이다.
모델이 과거 데이터를 보고 입력과 출력 간의 관계를 학습하여 새로운 데이터를 예측한다.
예제:
- 이메일이 스팸인지 아닌지 분류하는 모델 (이진 분류)
- 집 크기와 위치를 기반으로 집값을 예측하는 모델 (회귀 분석)

(2) 비지도 학습 (Unsupervised Learning)

정답(레이블)이 없는 데이터에서 패턴을 찾아내는 학습 방식이다.
데이터의 숨겨진 구조를 분석하여 유사한 그룹을 찾거나 특징을 요약한다.
예제:
- 고객을 유사한 그룹으로 분류하는 모델 (군집 분석)
- 문서에서 주요 주제를 자동으로 추출하는 모델 (토픽 모델링)

(3) 강화 학습 (Reinforcement Learning, RL)

보상을 최대화하는 방향으로 스스로 학습하는 방식이다.
행동(Action)을 하면 보상(Reward) 또는 패널티(Penalty)를 받으며 점점 더 좋은 전략을 학습한다.
예제:
- 알파고가 바둑을 학습하는 방식
- 자율주행 자동차가 주행하면서 최적의 경로를 학습하는 방식

3. 머신러닝의 핵심 과정

머신러닝 프로젝트는 보통 다음과 같은 단계로 진행된다.

(1) 데이터 수집 및 전처리

데이터를 모으고, 누락된 값이나 이상치를 처리하여 깨끗한 데이터셋을 만든다.

(2) 데이터 탐색 및 시각화

데이터를 분석하고 시각화하여 특성을 이해한다.

(3) 모델 선택 및 학습

적절한 머신러닝 알고리즘을 선택하고 데이터를 학습시킨다.

(4) 모델 평가 및 개선

학습된 모델의 성능을 평가하고, 과적합(Overfitting) 등을 방지하기 위해 최적화한다.

(5) 모델 배포 및 활용

완성된 모델을 실제 환경에서 사용한다.

4. 머신러닝이 왜 중요한가?

자동화 가능: 사람이 일일이 규칙을 만들지 않아도 자동으로 학습할 수 있다.
데이터 활용 극대화: 데이터를 통해 중요한 인사이트를 얻을 수 있다.
다양한 산업에서 활용 가능: 의료, 금융, 제조, IT 등 거의 모든 산업에서 활용된다.

5. 간단한 예제 코드 (지도 학습: 선형 회귀)

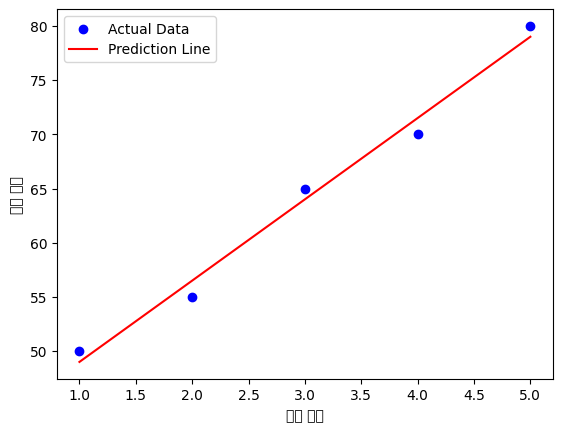
아래는 머신러닝의 대표적인 기법인 선형 회귀(Linear Regression)를 사용하여, 공부 시간(X)과 시험 점수(Y)의 관계를 예측하는 코드이다.

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

# 1. 데이터 준비 (공부 시간 X, 시험 점수 Y)

X = np.array([[1], [2], [3], [4], [5]]) # 공부 시간 (시간)

Y = np.array([50, 55, 65, 70, 80]) # 시험 점수 (점수)

# 2. 모델 생성 및 학습

model = LinearRegression() # 선형 회귀 모델 생성

model.fit(X, Y) # 모델 학습

# 3. 예측

predicted_score = model.predict([[6]]) # 공부 6시간 했을 때 예측 점수

print(f"공부 6시간 했을 때 예상 점수: {predicted_score[0]:.2f}점")

# 4. 결과 시각화

plt.scatter(X, Y, color='blue', label="Actual Data") # 실제 데이터

plt.plot(X, model.predict(X), color='red', label="Prediction Line") # 예측 선

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.legend()

plt.show()

공부 6시간 했을 때 예상 점수: 86.50점

6. 정리

머신러닝은 데이터를 통해 스스로 학습하는 기술이다.
지도 학습, 비지도 학습, 강화 학습의 세 가지 주요 유형이 있다.
머신러닝의 과정은 데이터 수집 → 모델 학습 → 평가 → 배포로 진행된다.
다양한 산업에서 활용되며, 자동화 및 데이터 활용을 극대화할 수 있다.

회귀분석(Regression Analysis)란?

회귀분석은 연속적인 숫자 값(수치형 데이터)을 예측하는 머신러닝 기법이다.
즉, 입력 변수(독립 변수, X)와 출력 변수(종속 변수, Y) 간의 관계를 찾아서, 새로운 입력 값에 대한 예측을 수행하는 기법이다.

1. 회귀분석의 핵심 개념

(1) 입력 변수(X)와 출력 변수(Y)
- 입력 변수(독립 변수, X): 예측에 사용되는 값 (예: 공부 시간, 광고 비용)
- 출력 변수(종속 변수, Y): 예측하고자 하는 값 (예: 시험 점수, 매출액)
예제:
- **공부 시간(X)**이 늘어나면 **시험 점수(Y)**도 증가할 가능성이 있다.
- **집 크기(X)**가 커지면 **집 가격(Y)**도 높아질 가능성이 있다.
(2) 선형 관계(Linear Relationship)
- 회귀 분석에서는 보통 입력 변수(X)와 출력 변수(Y) 사이의 수학적 관계를 찾는다.
- 예를 들어, 공부 시간이 늘어날수록 시험 점수가 증가하는 패턴을 찾을 수 있다.
(3) 수학적 표현 (일반적인 회귀 모델)Y=aX+bY = aX + b
- aa (기울기, 회귀 계수): X가 1 증가할 때 Y가 얼마나 증가하는지 나타냄.
- bb (절편): X가 0일 때 Y의 값.
회귀 분석에서는 입력 X를 기반으로 Y를 예측하는 함수(모델)를 만든다.
대표적인 수식은 직선 방정식이다.

2. 회귀분석의 주요 종류

(1) 단순 선형 회귀 (Simple Linear Regression)

입력 변수(X)가 1개인 경우.
예제:
- 공부 시간(X) → 시험 점수(Y)
- 광고 비용(X) → 매출액(Y)

수식:

Y=aX+bY = aX + b

데이터의 관계를 직선(1차 함수)으로 표현
수식:Y=aX+bY = aX + b
- aa : 기울기 (slope) → X가 1 증가할 때 Y의 변화량
- bb : 절편 (intercept) → X가 0일 때 Y 값
예제: 공부 시간(X) → 시험 점수(Y) 예측

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

# 데이터 준비

X = np.array([[1], [2], [3], [4], [5]]) # 공부 시간

Y = np.array([50, 55, 65, 70, 80]) # 시험 점수

# 모델 생성 및 학습

model = LinearRegression()

model.fit(X, Y)

# 예측 및 결과 출력

predicted_score = model.predict([[6]])

print(f"공부 6시간 했을 때 예상 점수: {predicted_score[0]:.2f}점")

# 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.plot(X, model.predict(X), color='red', label="Prediction Line")

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.legend()

plt.show()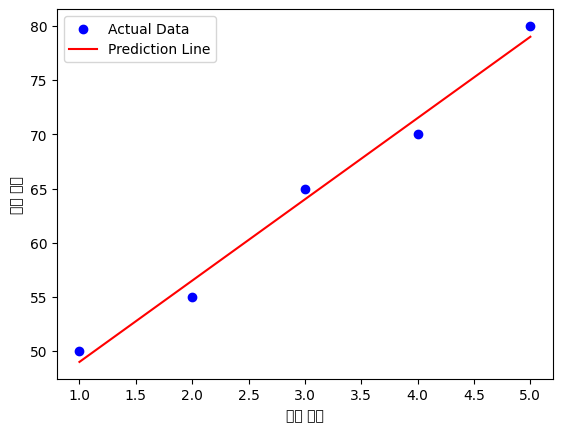

(2) 다중 선형 회귀 (Multiple Linear Regression)

독립 변수가 2개 이상인 경우
입력 변수가 여러 개인 경우.

예제:
- 공부 시간(X1), 수면 시간(X2) → 시험 점수(Y)
- 광고 비용(X1), 제품 가격(X2), 할인율(X3) → 매출액(Y)

수식:

Y=a1X1+a2X2+a3X3+...+bY = a_1X_1 + a_2X_2 + a_3X_3 + ... + b

여러 개의 변수가 종속 변수에 영향을 주는 관계를 분석
수식: Y=a1X1+a2X2+a3X3+...+bY = a_1X_1 + a_2X_2 + a_3X_3 + ... + b
- 예제:
  - 집값 예측 모델:
    - X1X_1 (평수), X2X_2 (방 개수), X3X_3 (위치) → YY (집값)
- from sklearn.linear_model import LinearRegression
  
  # 데이터 준비 (평수, 방 개수, 위치)
  
  X = np.array([[50, 2, 1], [70, 3, 2], [90, 4, 3], [120, 5, 4]]) # 독립 변수
  
  Y = np.array([200, 300, 400, 500]) # 집값
  
  # 모델 학습
  
  model = LinearRegression() # 선형 회귀 모델 생성
  
  model.fit(X, Y) # 학습 (X → Y 관계 학습)
  
  # 예측
  
  new_house = np.array([[80, 3, 2]]) # 평수: 80, 방 개수: 3, 위치: 2
  
  predicted_price = model.predict(new_house)
  
  print(f"예측된 집값: {predicted_price[0]:.2f}만원")
- import pandas as pd
- 결과
- 예측된 집값: 300.00만원
- # 이 값을 확인하면 모델이 어떻게 예측값을 계산하는지 알 수 있다.
  
  print("기울기 (coefficients):", model.coef_)
  
  print("절편 (intercept):", model.intercept_)
```
기울기 (coefficients): [-4.04073143e-16  5.00000000e+01  5.00000000e+01]
절편 (intercept): 49.999999999999886
```

기울기 값 -4.04 × 10⁻¹⁶은 거의 0에 가까운 값이다.

이는 X1(평수)이 종속 변수 Y(집값)에 거의 영향을 주지 않는다는 것을 의미한다.
선형 회귀에서 계산할 때 수학적으로 0이 되어야 하는 값이 부동소수점 연산 오차로 인해 아주 작은 값으로 표현된 것.

절편(Intercept)이란?

X1 = 0, X2 = 0, X3 = 0일 때 Y의 값
즉, 모든 독립 변수가 0일 때 집값이 50 (만원 단위) 라는 의미이다.
하지만, X1=0(평수가 0)인 경우는 현실적으로 말이 안 되므로 이 절편 값은 해석할 의미가 크지 않다.

(3) 다항 회귀 (Polynomial Regression)

데이터가 선형 관계가 아닌 경우, 직선이 아닌 곡선 관계를 가질 때 사용하는 방법.
예제:
- 자동차 속도(X) → 연료 소비량(Y) (속도가 너무 높거나 낮을 때 연료 소모가 달라짐)
- 공부 시간(X) → 성적(Y) (너무 많이 공부하면 피로 때문에 성적이 떨어질 수도 있음)

수식:

Y=aX2+bX+cY = aX^2 + bX + c

2차, 3차 이상의 다항식을 사용하여 복잡한 패턴을 학습
수식 (2차 회귀):Y=aX2+bX+cY = aX^2 + bX + c
예제: 자동차 속도(X) → 제동 거리(Y) 예측

from sklearn.preprocessing import PolynomialFeatures

from sklearn.pipeline import make_pipeline

# 데이터

X = np.array([[10], [20], [30], [40], [50]]) # 속도

Y = np.array([5, 20, 60, 130, 210]) # 제동 거리

# 다항 회귀 모델 (2차)

model = make_pipeline(PolynomialFeatures(2), LinearRegression())

model.fit(X, Y)

# 예측

predicted_distance = model.predict([[35]])

print(f"속도 35km/h에서 예상 제동 거리: {predicted_distance[0]:.2f}m")

# 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.plot(X, model.predict(X), color='red', label="Polynomial Regression")

plt.xlabel("속도 (km/h)")

plt.ylabel("제동 거리 (m)")

plt.legend()

plt.show()

(4) 로지스틱 회귀 (Logistic Regression) - 분류 모델

로지스틱 회귀는 회귀라는 이름이 붙었지만, 실제로는 분류 문제에 사용됨
회귀라는 이름을 가졌지만, 결과값이 0 또는 1 (참/거짓) 같은 분류 문제에 사용됨.

예제:
- 이메일이 스팸(1)인지 아닌지(0) 예측
- 환자가 질병이 있는지(1) 없는지(0) 예측

수식:

Y=11+e−(aX+b)Y = \frac{1}{1 + e^{-(aX + b)}}

결과값이 0~1 사이의 확률로 변환됨.

결과값이 0 또는 1 같은 이진 분류(Yes/No, True/False 등)
예제: 이메일이 스팸인지 아닌지(0 또는 1) 분류

from sklearn.linear_model import LogisticRegression

# 데이터 (단순 예제)

X = np.array([[1], [2], [3], [4], [5]]) # 이메일 단어 개수

Y = np.array([0, 0, 0, 1, 1]) # 0: 정상, 1: 스팸

# 모델 학습

model = LogisticRegression()

model.fit(X, Y)

# 예측

predicted_class = model.predict([[3.5]])

print(f"단어 개수 3.5개일 때 예상 분류: {'스팸' if predicted_class[0] == 1 else '정상'}")

단어 개수 3.5개일 때 예상 분류: 정상

3. 회귀분석 평가 지표

모델의 성능을 평가하는 지표:

회귀 분석은 다양한 분야에서 사용된다.

분야 / 예제

마케팅	광고 비용 → 매출액 예측
경제	주택 크기 → 집 가격 예측
교육	공부 시간 → 시험 점수 예측
헬스케어	환자 나이, 체중 → 혈압 예측

R²(결정계수): 0~1 사이 값으로 1에 가까울수록 모델 성능이 좋음
MSE(평균제곱오차): 작은 값일수록 예측 오류가 적음
RMSE(제곱근 평균제곱오차): MSE보다 직관적인 오류 측정값

from sklearn.metrics import mean_squared_error, r2_score

# 예측값

Y_pred = model.predict(X)

# 평가

mse = mean_squared_error(Y, Y_pred)

r2 = r2_score(Y, Y_pred)

print(f"MSE: {mse:.2f}, R²: {r2:.2f}")

MSE: 0.00, R²: 1.00

4. 단순 선형 회귀 코드 예제

아래는 공부 시간(X)에 따른 시험 점수(Y)를 예측하는 단순 선형 회귀 모델이다.

(1) 데이터 준비 및 시각화

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

# 데이터 준비

X = np.array([[1], [2], [3], [4], [5]]) # 공부 시간

Y = np.array([50, 55, 65, 70, 80]) # 시험 점수

# 데이터 시각화

plt.scatter(X, Y, color='blue', label="Actual Data")

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.legend()

plt.show()

(2) 모델 학습 및 예측

# 모델 생성 및 학습

model = LinearRegression()

model.fit(X, Y)

# 예측 수행

predicted_score = model.predict([[6]]) # 공부 6시간 했을 때 예측 점수

print(f"공부 6시간 했을 때 예상 점수: {predicted_score[0]:.2f}점")

공부 6시간 했을 때 예상 점수: 86.50점

(3) 결과 시각화

# 예측 결과 시각화

plt.scatter(X, Y, color='blue', label="Actual Data") # 실제 데이터

plt.plot(X, model.predict(X), color='red', label="Prediction Line") # 예측 선

plt.xlabel("공부 시간")

plt.ylabel("시험 점수")

plt.legend()

plt.show()

5. 회귀 분석에서 중요한 개념

(1) 과적합(Overfitting) vs. 과소적합(Underfitting)

과적합: 학습 데이터에 너무 딱 맞는 모델 → 새로운 데이터에 대한 예측 성능이 나쁨.
과소적합: 너무 단순한 모델 → 데이터의 패턴을 제대로 학습하지 못함.

(2) 성능 평가 지표

MSE (Mean Squared Error, 평균 제곱 오차)
- 값이 작을수록 예측이 정확함.
- MSE=1n∑(실제값−예측값)2\text{MSE} = \frac{1}{n} \sum (실제값 - 예측값)^2
R² Score (결정 계수, 모델의 설명력 측정)
- 0~1 사이의 값으로, 1에 가까울수록 좋은 모델.

from sklearn.metrics import mean_squared_error, r2_score

Y_pred = model.predict(X)

mse = mean_squared_error(Y, Y_pred)

r2 = r2_score(Y, Y_pred)

print(f"평균 제곱 오차(MSE): {mse:.2f}")

print(f"결정 계수(R² Score): {r2:.2f}")

평균 제곱 오차(MSE): 1.50

결정 계수(R² Score): 0.99

6. 정리

회귀 분석은 숫자 예측을 위한 머신러닝 기법이다.
단순 선형 회귀, 다중 선형 회귀, 다항 회귀 등 다양한 방식이 있다.
성능 평가를 위해 MSE, R² Score 등을 사용한다.
과적합을 방지하고 일반화 성능을 높이는 것이 중요하다.

1. MSE (Mean Squared Error, 평균 제곱 오차)

MSE는 예측값과 실제값의 차이(오차)를 제곱하여 평균낸 값이다.

(1) 수식

MSE=1n∑i=1n(yi−y^i)2MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

yiy_i : 실제값 (Real Value)
y^i\hat{y}_i : 예측값 (Predicted Value)
nn : 데이터 개수

(2) 특징

값이 작을수록 모델의 예측이 정확함을 의미한다.
오차를 제곱하기 때문에 큰 오차일수록 더 큰 패널티를 받는다.
단위가 예측값의 단위 제곱이므로, 해석할 때 주의가 필요하다. (예: 원래 값이 kg이면 MSE 단위는 kg²)

from sklearn.metrics import mean_squared_error

# 실제값과 예측값

Y_real = [50, 55, 65, 70, 80] # 실제 시험 점수

Y_pred = [52, 54, 63, 72, 78] # 예측된 시험 점수

# MSE 계산

mse = mean_squared_error(Y_real, Y_pred)

print(f"MSE: {mse:.2f}")

MSE: 3.40

2. R² Score (결정 계수, 모델 설명력)

R² Score는 모델이 실제 데이터를 얼마나 잘 설명하는지 나타내는 지표로, 0에서 1 사이의 값을 가진다.

(1) 수식

R2=1−∑(yi−y^i)2∑(yi−yˉ)2R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2}

yiy_i : 실제값
y^i\hat{y}_i : 예측값
yˉ\bar{y} : 실제값의 평균
분자는 모델이 만든 예측값이 얼마나 실제값과 차이가 있는지를 나타냄.
분모는 평균값으로 예측했을 때의 오차를 의미.

(2) 특징

R2=1R^2 = 1 → 모델이 완벽하게 예측한 경우
R2=0R^2 = 0 → 모델이 아예 예측하지 못하고 평균값 수준의 성능을 낸 경우
R2<0R^2 < 0 → 모델이 평균값보다도 성능이 안 좋은 경우 (잘못된 모델)

from sklearn.metrics import r2_score

# 실제값과 예측값

Y_real = [50, 55, 65, 70, 80]

Y_pred = [52, 54, 63, 72, 78]

# R² Score 계산

r2 = r2_score(Y_real, Y_pred)

print(f"R² Score: {r2:.2f}")

R² Score: 0.97

정리

MSE(평균 제곱 오차): 예측값과 실제값의 차이를 제곱하여 평균낸 값. 값이 작을수록 좋은 모델.
R² Score(결정 계수): 모델이 데이터를 얼마나 잘 설명하는지 나타내는 지표. 1에 가까울수록 좋은 모델.

KNN 모델과 SVM 모델에서 One-Hot Encoding 이 필요한 이유

1. One-Hot Encoding이 필요한 이유

✔ KNN과 SVM 모두 수치 데이터를 기반으로 작동하는 머신러닝 모델이기 때문

KNN (K-최근접 이웃)

유클리드 거리(Euclidean Distance) 를 기반으로 분류
문자 데이터가 있으면 거리를 계산할 수 없음 → One-Hot Encoding 필요

SVM (Support Vector Machine)

결정 경계(Hyperplane)를 학습하여 분류
숫자 데이터만 학습 가능 → One-Hot Encoding 필요

2. One-Hot Encoding을 적용하는 이유

✔ 범주형(문자) 데이터를 숫자로 변환하면서, 불필요한 크기 관계를 없애기 위해

원본 데이터 (문자형) / 라벨 인코딩 (X) / 원-핫 인코딩 (O)

male, female	0, 1 (순서 개념이 생김)	[1,0], [0,1] (순서 없음)
S, C, Q	0, 1, 2	[1,0,0], [0,1,0], [0,0,1]

✔ 라벨 인코딩(X) → 숫자가 크기 비교되므로 부적절
✔ One-Hot Encoding(O) → 독립적인 열을 만들어 크기 비교 문제 해결

3. 정리

1. KNN과 SVM 모두 숫자 데이터만 학습 가능 → 문자 데이터를 변환해야 함
2. KNN은 거리 기반 모델이므로, One-Hot Encoding을 적용해야 정확한 거리 계산 가능
3. SVM은 결정 경계를 찾는 모델이라, 범주형 데이터를 숫자로 변환해야 학습 가능
4. One-Hot Encoding을 적용하면 범주형 데이터의 크기 비교 문제를 방지할 수 있음

따라서, KNN과 SVM에서는 One-Hot Encoding을 공통적으로 적용해야 한다.

KNN (K-Nearest Neighbors, K-최근접 이웃)란?

KNN은 거리를 기반으로 데이터의 패턴을 찾는 비지도 학습 및 지도 학습 모델이다.

새로운 데이터가 들어오면 가까운 데이터(K개)를 찾아 그 데이터들의 평균값(회귀) 또는 다수결(분류)로 결과를 결정한다.
단순하지만 강력한 알고리즘으로, 초보자가 이해하기 쉬운 머신러닝 기법 중 하나이다.

1. KNN의 기본 개념

KNN은 데이터 간 거리를 계산하여 새로운 데이터의 클래스를 예측한다.

(1) K개의 가장 가까운 이웃 찾기

새로운 데이터가 주어지면, 기존 데이터 중 가장 가까운 K개의 데이터를 선택한다.
가까운 K개 데이터를 통해 새로운 데이터의 클래스(분류) 또는 값을 예측(회귀)한다.

(2) 거리 계산 방법

KNN은 **유클리드 거리(Euclidean Distance)**를 가장 많이 사용한다.

d(A,B)=(x2−x1)2+(y2−y1)2d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

두 점 A(x1,y1)A(x_1, y_1)와 B(x2,y2)B(x_2, y_2) 사이의 거리 계산
차원이 높을 경우 맨해튼 거리(Manhattan Distance), 코사인 유사도(Cosine Similarity) 등을 사용할 수도 있다.

(3) K 값의 선택 (Hyperparameter)

K가 너무 작으면(1~3): 노이즈(이상치)에 영향을 받아 과적합(Overfitting) 가능성이 높아진다.
K가 너무 크면: 너무 많은 데이터를 고려하여 평균적인 값이 나오므로 패턴을 제대로 반영하지 못할 수 있다.

K값은 보통 홀수(3, 5, 7 등)로 설정하며, 데이터의 크기와 분포에 따라 최적의 K를 찾아야 한다.

2. KNN의 유형

KNN은 분류(Classification)와 회귀(Regression) 모두 가능하다.

(1) KNN 분류 (KNN Classification)

가장 가까운 K개의 데이터 중 **다수결(Majority Voting)**로 클래스를 결정.
예제:
- 스팸 메일 분류 (스팸/일반)
- 고객의 구매 여부 예측 (구매/미구매)

설명:

빨간색 원(새로운 데이터)의 클래스를 예측하려고 할 때,
- K=3이면, 가까운 3개의 데이터 중 다수가 초록색 → 초록색으로 분류
- K=5이면, 가까운 5개의 데이터 중 다수가 파란색 → 파란색으로 분류

(2) KNN 회귀 (KNN Regression)

가장 가까운 K개의 데이터들의 평균을 계산하여 값 예측.
예제:
- 집 크기를 기반으로 집 가격 예측
- 온도 데이터를 기반으로 내일의 기온 예측

3. KNN 알고리즘 동작 과정

새로운 데이터 포인트를 받는다.
기존 데이터와의 거리를 계산한다.
가장 가까운 K개의 데이터를 찾는다.
(분류) K개의 데이터 중 가장 많은 클래스로 예측.
(회귀) K개의 데이터의 평균값을 예측값으로 사용.
결과를 출력한다.

4. KNN 구현 (Python 코드)

KNN을 활용하여 붓꽃(Iris) 데이터 분류를 수행해보자.

(1) 데이터 불러오기 및 전처리

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import StandardScaler

from sklearn.neighbors import KNeighborsClassifier

from sklearn.metrics import accuracy_score

# 1. 데이터 로드

iris = load_iris()

X, y = iris.data, iris.target # 입력 데이터(X), 정답(y)

# 2. 데이터 분할 (훈련 80%, 테스트 20%)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 데이터 정규화 (거리 기반 알고리즘이므로 스케일링 필수)

scaler = StandardScaler()

X_train = scaler.fit_transform(X_train)

X_test = scaler.transform(X_test)

(2) KNN 모델 학습 및 예측

# 4. KNN 모델 생성 (K=5)

knn = KNeighborsClassifier(n_neighbors=5)

knn.fit(X_train, y_train) # 모델 학습

# 5. 예측 수행

y_pred = knn.predict(X_test)

# 6. 정확도 평가

accuracy = accuracy_score(y_test, y_pred)

print(f"KNN 분류 정확도: {accuracy:.2f}")

KNN 분류 정확도: 1.00

(3) 최적의 K 찾기

import matplotlib.pyplot as plt

# 여러 개의 K값을 테스트하여 정확도 비교

k_values = range(1, 20)

accuracies = []

for k in k_values:

knn = KNeighborsClassifier(n_neighbors=k)

knn.fit(X_train, y_train)

y_pred = knn.predict(X_test)

accuracies.append(accuracy_score(y_test, y_pred))

# 그래프 그리기

plt.plot(k_values, accuracies, marker='o')

plt.xlabel("K 값")

plt.ylabel("정확도")

plt.title("K 값에 따른 KNN 정확도")

plt.show()

5. KNN의 장점과 단점

(1) 장점

단순하고 직관적: 쉽게 이해하고 구현할 수 있음.
학습 시간이 빠름: 학습 단계에서 단순히 데이터를 저장하는 것뿐이므로 빠름.
비선형 데이터에도 적용 가능: 곡선 형태의 데이터에도 유용함.

(2) 단점

예측 속도가 느림: 새로운 데이터가 들어올 때마다 모든 데이터와 거리 계산을 해야 하므로 데이터가 많으면 속도가 느려짐.
차원의 저주(The Curse of Dimensionality): 데이터 차원이 많아질수록 거리 계산이 어려워지고 성능이 저하됨.
K 값 설정이 중요: K를 잘못 설정하면 성능이 저하될 수 있음.

6. KNN이 잘 맞는 경우 & 잘 안 맞는 경우

KNN이 잘 맞는 경우

데이터가 **적당한 크기(수천 개 이하)**일 때
데이터가 균일하게 분포할 때 (군집이 명확하게 나뉠 때)
데이터의 차원이 낮을 때(2~10차원)

KNN이 잘 안 맞는 경우

데이터 개수가 너무 많을 때 (수십만 개 이상 → 속도가 느려짐)
차원이 너무 높을 때 (차원의 저주 문제 발생)
데이터가 복잡하게 얽혀 있을 때 (거리가 애매하게 나오면 성능이 저하됨)

7. 정리

KNN은 거리를 기반으로 데이터를 분류하거나 예측하는 알고리즘이다.
K개의 가장 가까운 데이터를 사용하여 다수결(분류) 또는 평균(회귀)으로 결과를 결정한다.
K값이 너무 작으면 과적합, 너무 크면 과소적합이 발생할 수 있다.
거리 기반 알고리즘이므로 데이터 정규화(스케일링)가 중요하다.
데이터가 많거나 차원이 높아지면 성능이 저하될 수 있다.

혼동 행렬(Confusion Matrix) 시각화

1. 혼동 행렬(Confusion Matrix)란?

모델이 예측한 결과와 실제값을 비교하여 얼마나 정확하게 분류했는지 나타내는 표
행(Row): 실제값(Actual label)
열(Column): 예측값(Predicted label)
각 칸에 예측이 맞거나 틀린 횟수가 표시됨
이진 분류(Negative(0), Positive(1))에서 자주 사용됨

2. 코드 실행 과정 설명

plt.figure(figsize=(8, 6))

그래프 크기를 (8, 6)로 설정

sns.heatmap(knn_matrix, annot=True, fmt='d', cmap='Blues',

xticklabels=['Negative', 'Positive'],

yticklabels=['Negative', 'Positive'])

knn_matrix: confusion_matrix(y_test, y_hat)를 통해 계산된 혼동 행렬 데이터
annot=True: 각 셀에 숫자 값 표시
fmt='d': 숫자 형식을 정수(d)로 설정
cmap='Blues': 파란색 계열 색상 지정
xticklabels=['Negative', 'Positive'] → 예측된 값 (가로축)
yticklabels=['Negative', 'Positive'] → 실제 값 (세로축)

plt.title('Confusion Matrix')

plt.ylabel('Actual label')

plt.xlabel('Predicted label')

plt.show()

그래프 제목, 축 레이블 설정 후 출력

3. 실행 후 결과 예시

예측: 0 (Negative)예측: 1 (Positive)

실제: 0 (Negative)	50 (TN)	5 (FP)
실제: 1 (Positive)	8 (FN)	41 (TP)

✔ 정확한 예측 (TN, TP) 값이 많을수록 모델이 잘 작동하는 것
✔ FP(False Positive)와 FN(False Negative)이 적을수록 모델이 신뢰할 수 있음

4. 핵심 개념 정리

1. 혼동 행렬(Confusion Matrix)은 예측값과 실제값을 비교하는 표
2. sns.heatmap()을 사용해 혼동 행렬을 시각화
3. 파란색(cmap='Blues')으로 시각적 가독성을 높임
4. 오차(FP, FN)를 분석하여 모델 성능을 평가할 수 있음

KNN을 포함한 모든 분류 모델의 성능을 쉽게 평가할 수 있다!

커널 밀도 추정(Kernel Density Estimation, KDE) 그래프

커널 밀도 그래프(KDE) 는 히스토그램을 부드럽게 변형한 형태로, 데이터의 분포를 더 직관적으로 파악할 수 있는 시각화 기법이다.

1. KDE 그래프의 핵심 개념

KDE는 확률 밀도 함수(PDF, Probability Density Function)를 추정하는 방법으로, 주어진 데이터의 분포를 매끄러운 곡선 형태로 표현한다.
즉, "데이터가 특정 구간에 존재할 확률이 얼마나 높은지" 를 부드러운 곡선으로 보여준다.

🔹 히스토그램 vs. KDE

히스토그램 vs. KDE

표현 방식	막대 그래프	곡선 그래프
부드러움	경계가 뚜렷함	연속적이고 부드러움
구간 개수 영향	bin 개수에 따라 형태 변화	밴드너비(bandwidth) 설정에 영향

2. KDE의 핵심 요소

KDE를 구성하는 주요 요소는 커널(Kernel) 과 밴드너비(Bandwidth) 두 가지다.

커널(Kernel)
- 데이터가 특정 위치에서 얼마나 영향을 미치는지를 결정하는 함수
- 가우시안(정규분포), 균등분포, 삼각형 함수 등의 형태가 있음
- 보통 가우시안(정규분포) 커널을 가장 많이 사용함
밴드너비(Bandwidth, h)
- KDE 그래프의 부드러움을 결정하는 매개변수
- 밴드너비가 크면 → 곡선이 부드럽고 범용적인 분포를 보임
- 밴드너비가 작으면 → 곡선이 데이터에 과적합(세밀하지만 과도하게 복잡)

밴드너비를 적절히 조절하는 것이 KDE의 핵심이다!

3. KDE 그래프 그리기 (Seaborn 활용)

Python의 seaborn.kdeplot() 을 사용하면 쉽게 KDE 그래프를 그릴 수 있다.

단일 변수 KDE 그래프

import seaborn as sns

import matplotlib.pyplot as plt

# 샘플 데이터 생성

tips = sns.load_dataset("tips")

# KDE 그래프 그리기

sns.kdeplot(data=tips, x="total_bill", fill=True)

plt.title("KDE Plot of Total Bill")

plt.show()

✔ fill=True 옵션을 사용하면 그래프 내부를 색칠할 수 있다.

4. KDE 그래프의 밴드너비 조절

밴드너비(bw_adjust)를 변경하여 KDE의 부드러움을 조절할 수 있다.

sns.kdeplot(data=tips, x="total_bill", fill=True, bw_adjust=0.5) # 더 세밀한 KDE

sns.kdeplot(data=tips, x="total_bill", fill=True, bw_adjust=2) # 더 부드러운 KDE

plt.legend(["bw_adjust=0.5", "bw_adjust=2"])

plt.title("Effect of Bandwidth on KDE Plot")

plt.show()

✔ bw_adjust 값을 작게 하면 그래프가 더 세밀하고, 크게 하면 더 부드럽게 표현된다.

5. KDE와 히스토그램 함께 그리기

KDE 그래프와 히스토그램을 함께 시각화하면 데이터를 더 직관적으로 파악할 수 있다.

sns.histplot(data=tips, x="total_bill", kde=True)

plt.title("Histogram with KDE")

plt.show()

✔ kde=True 옵션을 추가하면 히스토그램 위에 KDE 곡선을 함께 표시할 수 있다.

6. 다변량 KDE (2차원 KDE 그래프)

KDE는 2개의 연속형 변수를 비교할 때도 사용할 수 있다.

sns.kdeplot(data=tips, x="total_bill", y="tip", fill=True)

plt.title("2D KDE Plot")

plt.show()

✔ x="total_bill", y="tip"을 설정하면 두 변수 간의 분포를 2D 밀도 그래프로 시각화할 수 있다.

정리: KDE 그래프

1. KDE는 확률 밀도 함수(PDF)를 추정하는 그래프
2. 히스토그램보다 부드럽게 데이터 분포를 표현
3. 핵심 요소: 커널(Kernel)과 밴드너비(Bandwidth)
4. Seaborn의 kdeplot() 함수로 쉽게 시각화 가능
5. 밴드너비(bw_adjust)를 조절하여 그래프의 부드러움 조절 가능
6. 2D KDE 그래프를 활용하여 다변량 데이터의 분포도 분석 가능

SVM (Support Vector Machine, 서포트 벡터 머신)란?

SVM은 두 개 이상의 그룹을 나누는 초평면(Hyperplane)을 찾는 지도 학습 알고리즘이다.

주어진 데이터를 보고 가장 최적의 경계를 찾는 것이 목표이다.
분류(Classification)와 회귀(Regression) 모두 가능하지만, 주로 분류 문제에서 사용된다.

1. SVM의 핵심 개념

SVM이 어떻게 데이터를 분류하는지 이해하려면 초평면(Hyperplane)과 서포트 벡터(Support Vector) 개념을 알아야 한다.

(1) 초평면 (Hyperplane)

데이터를 두 개의 클래스로 나누는 결정 경계(Decision Boundary) 역할을 하는 선(2D) 또는 면(3D 이상)이다.
목표: 두 클래스를 가장 잘 나누는 최적의 초평면을 찾는 것.

(2) 서포트 벡터 (Support Vector)

초평면과 가장 가까운 데이터 포인트들.
이 점들이 결정 경계를 정의하고, 이 점들을 기준으로 초평면이 결정됨.
서포트 벡터가 바뀌면 초평면도 바뀌므로, SVM은 이 점들만 활용해 학습함 → 효율적!

(3) 마진 (Margin)

초평면과 서포트 벡터 사이의 거리.
마진이 클수록 일반화 성능이 좋아진다 (과적합 방지).
SVM은 마진이 최대가 되는 초평면을 찾는 것이 목표이다.

2. SVM의 동작 원리

초평면 후보들을 찾음
- 여러 개의 초평면이 있을 수 있지만, 가장 적절한 초평면을 찾아야 한다.
마진이 가장 큰 초평면 선택
- 서포트 벡터와 초평면 사이의 거리가 가장 큰 초평면을 선택.
초평면을 기준으로 분류 수행
- 새로운 데이터가 들어오면 초평면 기준으로 어느 쪽에 속하는지 판단.

3. SVM의 유형

SVM은 데이터의 특성에 따라 선형 SVM과 비선형 SVM으로 나뉜다.

(1) 선형 SVM (Linear SVM)

데이터가 직선(2D) 또는 평면(3D)으로 나눌 수 있는 경우.
단순한 직선으로 두 클래스를 나눌 수 있음.
예제: 이메일이 스팸인지 아닌지 분류.

(2) 비선형 SVM (Non-Linear SVM)

데이터가 선형으로 나눌 수 없을 때 커널 트릭(Kernel Trick)을 사용하여 변환.
예제: 꽃잎의 길이와 너비로 꽃의 종류 분류 (선형으로 나눌 수 없는 경우).

4. 커널 트릭(Kernel Trick)이란?

데이터가 선형으로 구분되지 않을 때, 저차원 데이터를 고차원 공간으로 변환하는 방법.
대표적인 커널 함수:
1. 선형 커널 (Linear Kernel) → 데이터가 선형으로 분리 가능할 때.
2. 다항식 커널 (Polynomial Kernel) → 곡선으로 데이터를 분리할 때.
3. RBF(방사 기저 함수) 커널 (Radial Basis Function Kernel) → 가장 많이 사용되며, 복잡한 경계를 만들 때 효과적.
4. 시그모이드 커널 (Sigmoid Kernel) → 뉴런의 활성 함수처럼 작동.

5. SVM 구현 (Python 코드)

붓꽃(Iris) 데이터를 사용하여 SVM 분류를 수행해보자.

(1) 데이터 준비 및 전처리

from sklearn import datasets

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import StandardScaler

from sklearn.svm import SVC

from sklearn.metrics import accuracy_score

# 1. 데이터 로드

iris = datasets.load_iris()

X, y = iris.data, iris.target

# 2. 데이터 분할 (훈련 80%, 테스트 20%)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 데이터 정규화 (SVM은 거리 기반 모델이므로 스케일링 필수)

scaler = StandardScaler()

X_train = scaler.fit_transform(X_train)

X_test = scaler.transform(X_test)

(2) SVM 모델 학습 및 예측

# 4. SVM 모델 생성 (RBF 커널 사용)

svm_model = SVC(kernel='rbf', C=1.0, gamma='scale') # C: 규제 파라미터, gamma: RBF 커널 파라미터

svm_model.fit(X_train, y_train) # 모델 학습

# 5. 예측 수행

y_pred = svm_model.predict(X_test)

# 6. 정확도 평가

accuracy = accuracy_score(y_test, y_pred)

print(f"SVM 분류 정확도: {accuracy:.2f}")

SVM 분류 정확도: 1.00

(3) 최적의 커널 및 C 값 찾기

import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import GridSearchCV

# 7. 하이퍼파라미터 튜닝 (C와 커널 비교)

param_grid = {'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf', 'poly']}

grid_search = GridSearchCV(SVC(), param_grid, cv=5)

grid_search.fit(X_train, y_train)

# 8. 최적의 하이퍼파라미터 출력

print(f"최적의 C 값: {grid_search.best_params_['C']}")

print(f"최적의 커널: {grid_search.best_params_['kernel']}")

최적의 C 값: 10

최적의 커널: linear

6. SVM의 장점과 단점

장점

고차원 데이터에서 강력한 성능
→ 특히 차원이 높은 데이터에서도 잘 작동.
과적합 방지
→ 마진을 최대화하는 방식이므로 일반화 성능이 좋음.
커널 트릭으로 복잡한 데이터도 학습 가능
→ 선형으로 구분되지 않는 데이터도 처리 가능.

단점

대용량 데이터에 비효율적
→ 훈련 시간이 오래 걸리므로 데이터가 많으면 비효율적.
하이퍼파라미터 튜닝이 필요
→ C 값, 커널 선택, gamma 값 등을 조정해야 최적의 성능을 얻을 수 있음.
해석이 어려움
→ 결정 경계가 복잡해지면 사람이 해석하기 어려워짐.

7. SVM이 잘 맞는 경우 & 잘 안 맞는 경우

SVM이 잘 맞는 경우

데이터가 선형적으로 또는 비선형적으로 잘 구분될 때.
차원이 높은 데이터일 때 (예: 유전자 데이터).
샘플 수가 적고, 특성(feature)이 많을 때.

SVM이 잘 안 맞는 경우

데이터가 너무 많을 때 (속도가 느려짐).
클래스 간 중첩(overlap)이 심한 경우 (다른 모델이 더 적합할 수 있음).
데이터가 노이즈가 많을 때.

8. 정리

SVM은 데이터의 경계를 찾아 분류하는 강력한 알고리즘.
초평면과 서포트 벡터를 기반으로 최적의 마진을 찾는 것이 핵심.
선형 SVM과 비선형 SVM이 있으며, 커널 트릭을 활용하면 복잡한 데이터도 처리 가능.
고차원 데이터에서 강력한 성능을 보이지만, 데이터가 많으면 속도가 느려질 수 있음

Decision Tree (의사 결정 나무)란?

Decision Tree(의사 결정 나무)는 데이터를 여러 개의 분기로 나누어 예측을 수행하는 지도 학습 알고리즘이다.

분류(Classification)와 회귀(Regression) 모두 가능
데이터를 **여러 개의 질문(조건)**을 통해 **분할(split)**하면서 학습

예제

"날씨가 맑은가?" → "예" → "테니스를 친다"
"날씨가 흐린가?" → "예" → "테니스를 친다"
"날씨가 비오는가?" → "예" → "테니스를 치지 않는다"

=> 이런 식으로 조건을 따라가며 최종 결론을 도출하는 방식!

1. Decision Tree의 기본 개념

(1) 루트 노드 (Root Node)

트리의 최상단 노드, 가장 처음 데이터를 나누는 기준.

(2) 내부 노드 (Internal Node)

데이터를 나누는 중간 단계의 조건 노드.

(3) 리프 노드 (Leaf Node)

최종적인 분류 결과 또는 예측 값.

(4) 분할 (Splitting)

데이터를 두 개 이상의 그룹으로 나누는 과정.

(5) 가지치기 (Pruning)

불필요한 노드를 제거하여 과적합(Overfitting)을 방지.

2. Decision Tree의 동작 과정

1️⃣ 데이터에서 가장 중요한 특성을 선택 (Gini, 엔트로피 등 활용)
2️⃣ 특성을 기준으로 데이터를 분할 (각각의 서브그룹 생성)
3️⃣ 각 서브그룹에서 다시 최적의 기준을 찾아 반복적으로 분할
4️⃣ 리프 노드에 도달하면 분류(또는 예측) 완료

3. 분할 기준 (특성 선택 방법)

(1) 지니 불순도 (Gini Impurity)

Gini=1−∑i=1npi2Gini = 1 - \sum_{i=1}^{n} p_i^2

특정 노드에서 클래스가 얼마나 섞여 있는지 측정.
값이 작을수록 좋은 분할 기준.

(2) 엔트로피 (Entropy)

Entropy=−∑i=1npilog⁡2piEntropy = - \sum_{i=1}^{n} p_i \log_2 p_i

불확실성을 측정하며, 값이 작을수록 순수한 노드.
정보 이득(Information Gain)을 사용하여 특성을 선택.

4. Decision Tree 구현 (Python 코드)

(1) 데이터 로드 및 전처리

from sklearn import datasets

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier

from sklearn.metrics import accuracy_score

import matplotlib.pyplot as plt

from sklearn.tree import plot_tree

# 1. 데이터 로드 (붓꽃 데이터)

iris = datasets.load_iris()

X, y = iris.data, iris.target

# 2. 데이터 분할 (훈련 80%, 테스트 20%)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

(2) Decision Tree 모델 학습 및

# 3. 모델 생성 (Gini 기준, 최대 깊이 제한)

dt_model = DecisionTreeClassifier(criterion="gini", max_depth=3, random_state=42)

dt_model.fit(X_train, y_train) # 모델 학습

# 4. 예측 수행

y_pred = dt_model.predict(X_test)

# 5. 정확도 평가

accuracy = accuracy_score(y_test, y_pred)

print(f"Decision Tree 정확도: {accuracy:.2f}")

Decision Tree 정확도: 1.00

(3) 트리 시각화

plt.figure(figsize=(10, 6))

plot_tree(dt_model, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)

plt.show()

과대적합(Overfitting)이란?

1. 과대적합(Overfitting)의 정의

과대적합(Overfitting)은 머신러닝 모델이 학습 데이터(training data)에는 너무 잘 맞지만, 새로운 데이터(test data)에는 일반화되지 않는 현상을 의미한다.
즉, 모델이 훈련 데이터의 패턴뿐만 아니라 노이즈까지 학습하여 예측 성능이 저하되는 문제이다.

2. 과대적합의 특징

훈련 데이터에서는 높은 성능을 보이지만, 테스트 데이터에서는 성능이 떨어진다.
모델이 너무 복잡하여 불필요한 패턴까지 학습한다.
일반화 성능이 낮아 새로운 데이터에서 오차가 커진다.

(예제) 과대적합의 예시

학생이 기출문제(훈련 데이터)만 반복적으로 공부하여 만점을 받지만, 새로운 시험(테스트 데이터)에서는 낮은 점수를 받는 경우.
AI 모델이 얼굴 인식을 학습할 때 훈련 데이터에만 존재하는 특정 배경까지 학습하여 새로운 환경에서는 잘 작동하지 않는 경우.

3. 과대적합과 과소적합(Underfitting) 비교

머신러닝 모델은 과소적합(Underfitting)과 과대적합(Overfitting) 사이에서 적절한 균형을 맞춰야 한다.

➡ 최적의 모델은 과소적합과 과대적합 사이에서 균형을 맞춘 모델이다.

4. 과대적합이 발생하는 원인

(1) 데이터 관련 원인

훈련 데이터가 너무 적거나 편향되어 있는 경우
노이즈가 많은 데이터를 학습한 경우
훈련 데이터와 테스트 데이터의 분포가 다를 경우

(2) 모델 관련 원인

모델이 너무 복잡한 경우 (너무 많은 파라미터, 높은 차수의 다항 회귀 등)
특성이 너무 많아 불필요한 변수를 학습한 경우
훈련을 너무 오래 해서(에포크 수가 많아서) 훈련 데이터에 최적화된 경우

5. 과대적합 해결 방법

과대적합을 방지하기 위해서는 모델을 단순화하거나, 일반화 성능을 향상시키는 기법을 사용해야 한다.

(1) 데이터 관련 해결 방법

더 많은 데이터를 수집하여 학습 데이터와 테스트 데이터의 차이를 줄인다.
**데이터 증강(Data Augmentation)**을 통해 데이터를 인위적으로 늘린다.
**특성 선택(Feature Selection)**을 통해 불필요한 변수를 제거한다.

(2) 모델 관련 해결 방법

1) 정규화(Regularization) 적용

L1 정규화(Lasso Regression): 중요하지 않은 특성의 가중치를 0으로 만들어 모델을 단순화.
L2 정규화(Ridge Regression): 큰 가중치를 억제하여 모델이 과도하게 복잡해지는 것을 방지.

from sklearn.linear_model import Ridge, Lasso

ridge = Ridge(alpha=1.0) # L2 정규화 적용

lasso = Lasso(alpha=0.1) # L1 정규화 적용

2) 교차 검증(Cross Validation) 활용

훈련 데이터와 검증 데이터를 여러 번 나누어 학습 및 평가하여 과대적합을 방지.

from sklearn.model_selection import cross_val_score

scores = cross_val_score(model, X, y, cv=5) # 5-fold 교차 검증

print(f"평균 정확도: {scores.mean():.4f}")

3) 훈련 데이터와 검증 데이터 분리

학습할 때 훈련 데이터(train)와 검증 데이터(validation)를 따로 설정하여 과대적합 여부를 확인.

from sklearn.model_selection import train_test_split

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

4) 조기 종료(Early Stopping) 적용

모델이 훈련 데이터에 너무 과적합되지 않도록 검증 데이터의 성능이 더 이상 개선되지 않으면 학습을 중단.

from tensorflow.keras.callbacks import EarlyStopping

early_stopping = EarlyStopping(monitor='val_loss', patience=5)

5) 모델 복잡도 줄이기

특성 수를 줄이거나 차원 축소(PCA) 를 적용하여 모델을 단순화할 수 있음.

from sklearn.decomposition import PCA

pca = PCA(n_components=5) # 주요 5개 차원만 선택

X_reduced = pca.fit_transform(X)

6) 드롭아웃(Dropout) 적용 (신경망 모델)

신경망 모델에서 일부 뉴런을 랜덤하게 제외하여 특정 패턴에 과적합되는 것을 방지.

from tensorflow.keras.layers import Dropout

model.add(Dropout(0.3)) # 30% 뉴런을 랜덤하게 비활성화

6. 과대적합을 확인하는 방법

과대적합을 진단하는 방법은 다음과 같다.

(1) 훈련 데이터와 테스트 데이터 성능 비교

훈련 데이터에서 높은 정확도(예: 98%)를 보이지만, 테스트 데이터에서 낮은 정확도(예: 70%)를 보이면 과대적합이 의심됨.

train_score = model.score(X_train, y_train)

test_score = model.score(X_test, y_test)

print(f"훈련 데이터 정확도: {train_score:.2f}")

print(f"테스트 데이터 정확도: {test_score:.2f}")

(2) 학습 곡선(Learning Curve) 확인

훈련 데이터에서는 손실(loss)이 줄어들지만, 검증 데이터에서는 손실이 증가하면 과대적합을 의심할 수 있음.

import matplotlib.pyplot as plt

plt.plot(train_losses, label="Train Loss")

plt.plot(val_losses, label="Validation Loss")

plt.legend()

plt.title("Training vs Validation Loss")

plt.show()

7. 결론

과대적합(Overfitting)은 모델이 훈련 데이터에 너무 최적화되어 일반화 성능이 떨어지는 현상을 의미한다.
훈련 데이터에서는 높은 성능을 보이지만, 새로운 데이터에서는 성능이 저하되는 것이 특징이다.
정규화, 교차 검증, 조기 종료, 드롭아웃, 특성 선택 등의 기법을 활용하여 과대적합을 방지할 수 있다.
과대적합을 방지하면서도 좋은 성능을 내는 것이 머신러닝 모델 개발의 핵심 목표이다.

5. 과적합(Overfitting) 문제 해결 (가지치기, 하이퍼파라미터 튜닝)

(1) 트리 깊이 제한 (max_depth)

너무 깊어지면 과적합 위험 → 적절한 max_depth 설정

(2) 최소 샘플 개수 제한 (min_samples_split, min_samples_leaf)

분할을 위해 필요한 최소 샘플 개수를 조정하여 가지치기 효과.

(3) 불필요한 특성 제거

중요하지 않은 특성을 제외하면 과적합 방지 가능.

6. Decision Tree의 장단점

장점

이해하기 쉬운 모델 (시각화 가능)
전처리가 거의 필요 없음 (스케일링 불필요)
빠른 학습 속도 (복잡한 데이터에서도 잘 작동)

단점

과적합 가능성 높음 (너무 깊은 트리는 성능 저하)
노이즈에 민감 (작은 변화에도 트리가 크게 바뀔 수 있음)
고차원 데이터에 비효율적 (Random Forest 같은 앙상블 기법 필요)

7. Decision Tree가 잘 맞는 경우 & 잘 안 맞는 경우

잘 맞는 경우

데이터가 **작거나 중간 크기(수천 개 이하)**일 때
데이터가 규칙적인 패턴을 가지고 있을 때
사람이 결과를 쉽게 해석해야 하는 경우 (예: 의학 진단)

잘 안 맞는 경우

데이터가 너무 많을 때 (과적합 위험)
고차원 데이터에서 성능이 떨어질 수 있음 (Random Forest 추천)
노이즈가 많은 데이터 (훈련 데이터에 민감)

8. 정리

Decision Tree는 데이터를 분할하면서 학습하는 강력한 지도 학습 알고리즘.
Gini, 엔트로피 등을 활용해 최적의 특성을 선택하여 분할.
과적합을 방지하기 위해 트리 깊이 제한(max_depth), 가지치기(min_samples_split) 등이 필요.
단순한 데이터에서는 강력하지만, 복잡한 데이터에서는 Random Forest나 XGBoost 같은 앙상블 기법이 더 효과적.

군집(Clustering)이란?

군집(Clustering)은 비지도 학습(unsupervised learning)의 대표적인 기법으로, 비슷한 데이터끼리 묶어 그룹을 만드는 방법이다.

군집화는 데이터에 대한 사전 정보(정답)가 없는 상태에서 패턴을 찾는 것이 목적이다.
데이터를 의미 있는 그룹(Cluster)으로 나눠서 분석하는 데 사용된다.

1. 군집 분석이 필요한 이유

군집 분석은 다양한 분야에서 활용된다.

활용 분야 / 예제

고객 세분화	쇼핑몰에서 고객을 VIP/일반 고객으로 나누기
이미지 분류	비슷한 색상의 사진을 자동으로 그룹화
이상 탐지	네트워크 보안에서 이상 패턴 탐지
유전자 분석	비슷한 유전자 패턴을 가진 그룹 찾기

2. 군집 분석의 주요 알고리즘

군집 분석에는 여러 가지 방법이 있지만, 대표적인 알고리즘 3가지를 알아보자.

(1) K-Means (K-평균 군집)

가장 널리 쓰이는 군집 알고리즘
데이터를 K개의 그룹으로 나누는 방식
군집 중심(centroid)을 설정하고 데이터를 반복적으로 그룹화

동작 과정

K개의 중심점을 임의로 선택
각 데이터를 가장 가까운 중심점으로 할당 → 그룹 형성
각 그룹의 평균을 새로운 중심점으로 설정
위 과정 반복 → 더 이상 중심점이 변하지 않으면 종료

장점 & 단점

빠르고 간단함
K값을 미리 정해야 함
원형(구형) 군집이 아닌 경우 성능 저하 가능

(2) 계층적 군집 분석 (Hierarchical Clustering)

데이터 간의 거리를 기반으로 트리 구조(Dendrogram)를 만들어 군집화하는 방식
상향식(Agglomerative) 또는 하향식(Divisive) 방법을 사용
- 상향식: 개별 데이터를 시작으로 점점 군집을 합침
- 하향식: 전체 데이터를 시작으로 점점 군집을 분할

장점 & 단점

군집 개수(K)를 미리 정할 필요 없음
군집 구조를 트리 형태로 시각화 가능
데이터 개수가 많으면 속도가 느려짐

(3) DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

밀도를 기반으로 군집을 찾는 알고리즘
특정 반경(ε) 내에서 최소 개수 이상의 점을 포함하는 밀집 지역을 군집으로 간주

장점 & 단점

비정형적인 군집에도 강함 (K-Means보다 유연함)
이상치(Outlier) 탐지가 가능
데이터 밀도 차이가 큰 경우 군집 탐색이 어려울 수 있음

3. K-Means 군집 분석 실습 (Python 코드)

(1) 데이터 준비 및 시각화

import numpy as np

import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

from sklearn.datasets import make_blobs

# 가상의 데이터 생성

X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 데이터 시각화

plt.scatter(X[:, 0], X[:, 1], s=50)

plt.title("원본 데이터")

plt.show()

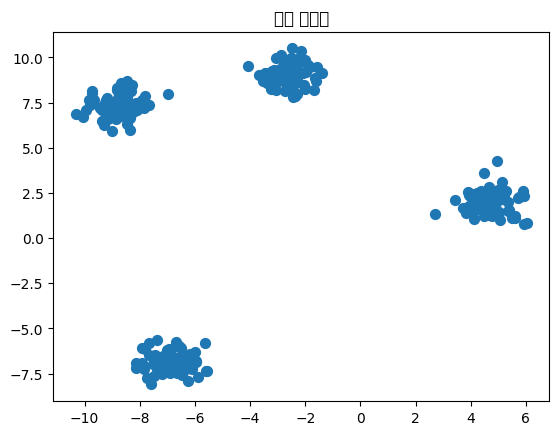
(2) K-Means 모델 적용

# K-Means 모델 생성 (K=4)

kmeans = KMeans(n_clusters=4, random_state=42)

y_kmeans = kmeans.fit_predict(X)

# 군집 시각화

plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis', s=50)

plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='X', s=200, label='Centroids')

plt.title("K-Means 클러스터링 결과")

plt.legend()

plt.show()

(3) 최적의 K 찾기 (Elbow Method)

# Elbow Method를 이용한 최적의 K 찾기

inertia = []

k_values = range(1, 10)

for k in k_values:

kmeans = KMeans(n_clusters=k, random_state=42)

kmeans.fit(X)

inertia.append(kmeans.inertia_)

# 결과 시각화

plt.plot(k_values, inertia, marker='o')

plt.xlabel("클러스터 개수 (K)")

plt.ylabel("Inertia (오차 제곱합)")

plt.title("Elbow Method를 이용한 최적의 K 찾기")

plt.show()

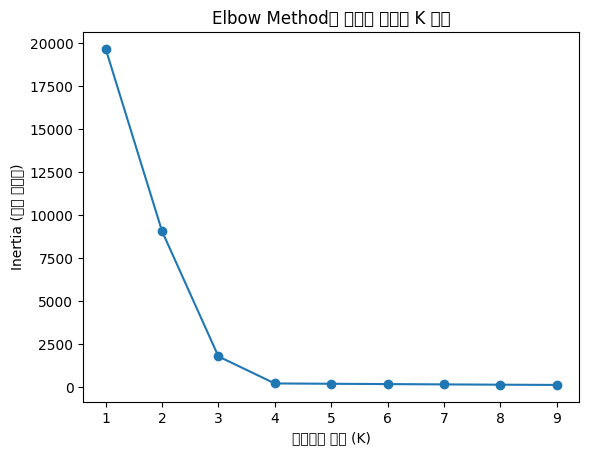
4. 군집 분석의 성능 평가

군집 분석은 정답(Label)이 없는 경우가 많기 때문에, 평가 방법이 지도 학습과 다름.

(1) 실루엣 점수 (Silhouette Score)

각 데이터가 같은 군집 내에서 얼마나 가까운지 측정
값이 1에 가까울수록 좋은 군집화
sklearn.metrics.silhouette_score 사용

from sklearn.metrics import silhouette_score

sil_score = silhouette_score(X, y_kmeans)

print(f"Silhouette Score: {sil_score:.2f}")

Silhouette Score: 0.88

5. 군집 분석의 장단점

장점

지도 학습이 필요 없음 → 레이블 없는 데이터에서도 유용
패턴 발견 가능 → 데이터의 숨겨진 구조를 찾을 수 있음
이상 탐지 가능 → 정상 데이터와 다른 이상 데이터를 감지 가능

단점

K-Means는 K를 미리 정해야 함
고차원 데이터에서 군집 품질이 저하될 수 있음
밀도 차이가 큰 데이터에서는 DBSCAN이 더 적합할 수 있음

6. 군집 분석이 잘 맞는 경우 & 잘 안 맞는 경우

잘 맞는 경우

비슷한 특성을 가진 그룹을 찾을 때
- 예: 고객 세분화, 유전자 분석
데이터가 비교적 균일하게 분포될 때
- 예: K-Means는 원형 군집에 강함

잘 안 맞는 경우

데이터 밀도가 다양할 때
- 예: K-Means는 비정형적인 군집을 잘 찾지 못함 (DBSCAN 추천)
군집 개수를 모를 때
- 예: 계층적 군집화(Hierarchical Clustering)가 더 적합할 수 있음

7. 정리

군집 분석은 데이터를 그룹으로 묶는 비지도 학습 기법.
K-Means, 계층적 군집 분석, DBSCAN 등이 대표적인 알고리즘.
K-Means는 빠르고 단순하지만, 군집 개수를 미리 정해야 함.
DBSCAN은 비정형적인 군집을 찾는 데 강력하지만, 밀도 차이가 클 경우 성능 저하 가능.
군집 분석의 성능은 실루엣 점수(Silhouette Score) 등을 활용하여 평가

데이터로 가치를 만드는 Steven, Follow on LinkedIn